2.4. Понятие обратной матрицы

Определение 1. Квадратная матрица А называется невырожденной (неособенной), если . В противном случае матрица А называется вырожденной (особенной).

Определение 2. Квадратная матрица называется обратной к матрице А, если выполняется равенство .

Замечание. Т.к. произведение коммутативно, то матрица имеет тот же порядок, что и матрица А.

Теорема. Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.

Необходимость. Пусть матрица А имеет обратную матрицу . Тогда

.

Отсюда следует , т.е. матрица А невырожденная.

Достаточность. Пусть матрица А невырожденная. Покажем, что существует такая матрица , что выполняется равенство . Для этого построим так называемую союзную матрицу матрице А, которая образуется из исходной матрицы заменой ее элементов на алгебраические дополнения с последующим транспонированием

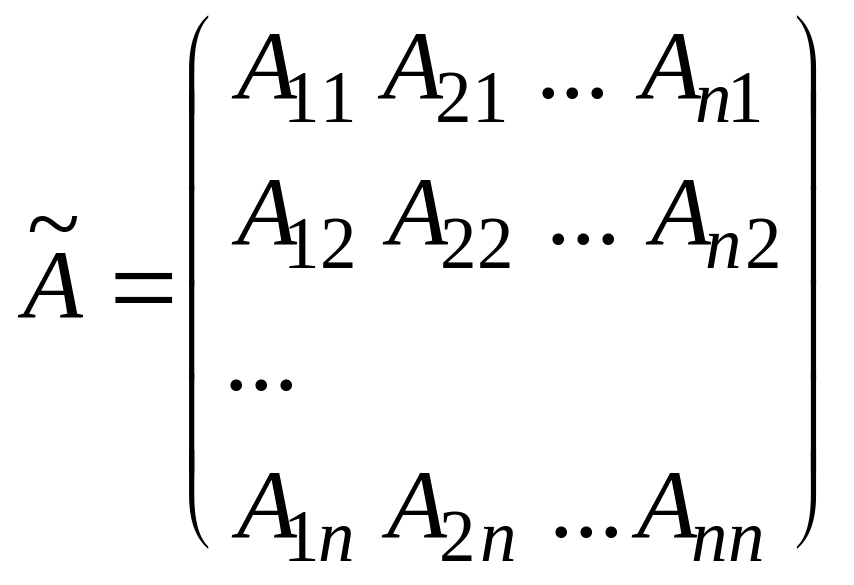
Вычислим произведение , используя правило умножения матриц и свойство 9 определителей

=

Аналогично устанавливается, что . Таким образом, искомая матрица имеет вид

Данная формула представляет явное выражение обратной матрицы.

2.5. Применение обратной матрицы к решению матричных уравнений

Метод обратной матрицы

Понятие обратной матрицы можно использовать для решения матричных уравнений. Например, в матричном уравнении неизвестная матрица Х находится умножением исходного уравнения слева на матрицу , справа на матрицу , т.е. . Т.к. , то .

Обычно рассмотренный метод обратной матрицы используют для решения квадратных систем линейных уравнений с определителем отличным от нуля. Действительно, квадратная система размерности n эквивалентна матричному уравнению

,

где

Ее решение имеет вид

.

Пример. Найдем решение системы 3-х уравнений методом обратной матрицы

Вычислим детерминант системы:

Найдем алгебраические дополнения:

Тогда обратная матрица системы имеет вид .

В результате имеем решение .

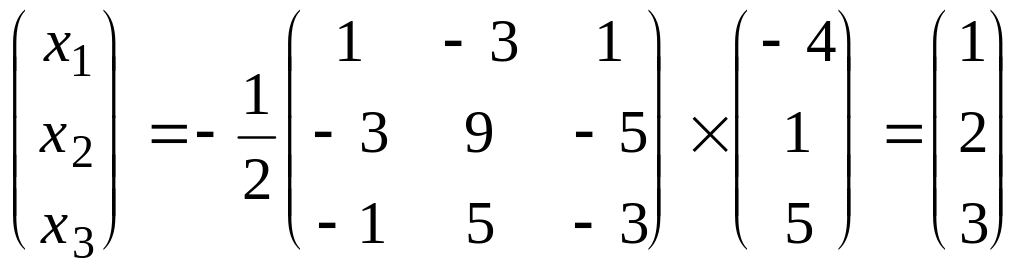Т.е. .

2.6. Ранг матрицы. Процедура нахождения ранга методом Гаусса

Определение 1. В матрице минор порядка называется базисным, если он отличен от нуля, а все миноры порядка равны нулю. Очевидно,

Замечание 1. В матрице может быть несколько различных базисных миноров, но они все имеют одинаковый порядок.

Замечание 2. Если миноры порядка равны нулю, то равны нулю миноры порядков тогда и миноры порядков и т.д.

Определение 2. Рангом матрицы называется порядок r базисного минора.

Oбозначается: , или просто r.

Перебирать все миноры матрицы в поисках базисного является громоздкой задачей. В этом случае удобно использовать теорему:

Теорема. Элементарные преобразования матрицы не меняют ее ранга.

Доказательство.

1. При умножении строки на число базисный минор либо не изменится, либо умножится на число , но ни один минор, равный нулю, не сделается отличным от нуля.

2. Пусть все миноры порядка равны нулю, сложим какие-либо две строки. Тогда минор равен cумме двух миноров порядка (если к строке, входящей в минор, прибавили строку, в него не входящую) или он равен сумме минора порядка и минора с двумя одинаковыми строками (если к строке, входящей в минор, прибавили строку, входящую в него). В обоих случаях он равен нулю. При этом ранг матрицы не понизится, т.к. в противном случае при обратном преобразовании (вычитании строк) он бы повысился).

3. При перестановке строк матрицы минор может изменить знак (если в него входят обе переставляемые строки) или замениться на минор, не более чем знаком отличающимся от другого минора той же матрицы (если содержит только одну из переставляемых строк) или вообще не измениться (если не содержит ни одной из переставляемых строк). Порядок базисного минора при этом не изменится.

Неизменность ранга при элементарных преобразованиях столбцов доказывается аналогично.

Наиболее эффективным методом вычисления ранга матрицы является

Метод Гаусса (вычисления ранга матрицы).

Пусть дана матрица и m<n. При помощи элементарных преобразований строк ее всегда можно привести к следующему виду: если r(A) = m, то m строк и m первых столбцов исходной матрицы имеют треугольный (ступенчатый) вид; если r(A) < m последние m-r(A) строк нулевые.

Пример. Найдем ранг матрицы А методом Гаусса:

.

Используя преобразования строк матрицы, приведем исходную матрицу А к ступенчатому виду

Отсюда следует, что .