2. Теория систем линейных уравнений
2.1. Понятие системы линейных уравнений
Системой линейных
m
уравнений с n
неизвестными
называется система следующих уравнений
(1)
где
величин
называются коэффициентами системы, m
величин
- свободными членами.
Система (1) называется
квадратной, если
,
т.е. число уравнений равно числу
неизвестных.
Система (1) называется однородной, если все ее свободные члены равны нулю. Если хотя бы один из этих членов отличен от нуля, то система (1) называется неоднородной.
Решением система (1) называется такая совокупность n чисел которая после подстановки их в систему обращает последнюю в систему m тождеств.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения.
Совместная система (1) называется определенной, если она имеет единственное решение, и неопределенной, если у нее существуют по крайней мере два различных решения.
Часто систему (1)
записывают в матричной форме
,
где
.
Матрица называется основной матрицей системы (1), В - матрица столбец свободных членов, Х - матрица столбец неизвестных членов.
2.2. Применение определителей к решению систем линейных уравнений. Правило Крамера
Рассмотрим квадратную систему размерности n
(1)
и предположим, что
Х=colon (
)
ее решение. Подставим решение в систему
(1), получим n
тождеств. Умножим 1-е тождество на
алгебраическое дополнение
элементов j-го
столбца основной матрицы А,
2-ое - на
и т.д., n-е
- на
и сложим все n
тождеств (cобирая
члены при
),
получим для любого j=1,2,...,n
равенство
(2)
или кратко
.
По свойству 9
определителей выражение в скобках равно
нулю, если
и равно определителю
матрицы А,
если
.
Теперь, заметим, что правая часть равна
определителю матрицы
А, у которой
вместо j-го
столбца стоит столбец свободных членов
.
Обозначим этот определитель
.
Тогда (2) запишется кратко
.
(3)
Мы пришли к теореме, которая носит название
Правило
Крамера.
Если решение
системы линейных уравнений (1) с
определителем
существует, то это решение единственное
и определяется формулами Крамера
.
(4)
Замечание. Анализируя соотношения (3) можно сделать следующее заключение о характере решений системы (1):
1)
если
,
то решение единственное;
2)
если
,
а хотя бы один из
,
то решений нет;
3)
если
и все
, то либо система несовместна, либо
решений бесконечное множество.
Пример.
Найдем решение системы 3-х уравнений с
неизвестными
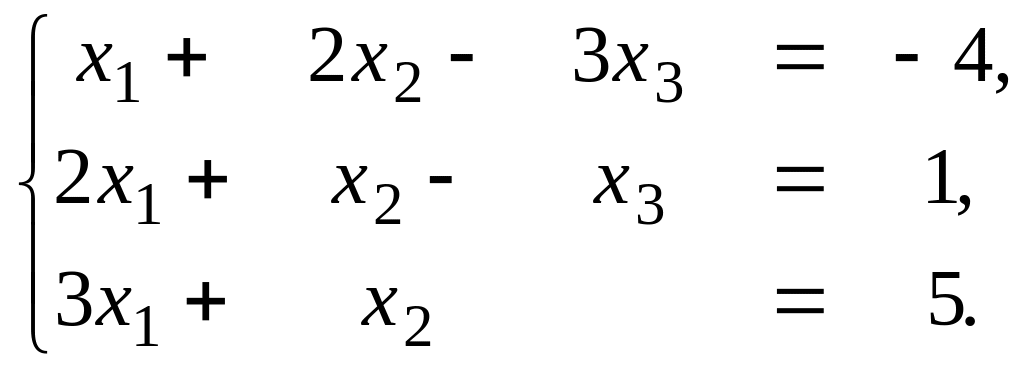
Вычислим определители
По формулам Крамера
2.3. Элементарные преобразования матрицы.
Теорема умножения определителей
Элементарными
преобразованиями матрицы
называются:
1.
умножение ее i-й
строки на число
;
2. прибавление к ее i-й строке любой другой j-й строки;
3. перестановка любых двух i-й и j-й строк;
4. аналогичные преобразования 1-3 для столбцов.
Замечание 1. Из определения элементарных преобразований следует сочетание операций, например, умножение j-й строки на число и прибавление ее к i-й строке.
Каждое из элементарных
преобразований 1-3
можно представить в виде произведения
некоторой матрицы
данную матрицу
,
где
1.
-
квадратная матрица порядка m,
получаемая из единичной Е
заменой в
i-й
строке единицы на число
;
при этом
;
2.
-
матрица, получаемая из единичной Е
заменой нулевого элемента в i-й
строке и j-м
столбце на единицу; при этом
;
3.
-
матрица, получаемая из единичной Е
перестановкой i-й
и j-й
строк; при этом
.
Замечание 2.
Для любой матрицы А
всегда можно подобрать р
матриц элементарных преобразований,
что
.
Для квадратной
матрицы А
легко проверяются соотношения
,
где S -
любая из трех перечисленных матриц.
Вообще имеет место более общее утверждение
Теорема. Для любых квадратных матриц А и В одного порядка справедливо равенство
.
Доказательство . Представим матрицу А в виде . Тогда
