1.4. Свойства определителей
Использование свойств определителей значительно упрощает их вычисление.
1.
При транспонировании матрицы
ее определитель не изменяется:
.
Это свойство означает полную равноправность строк и столбцов определителя. Поэтому следующие свойства будем формулировать только для строк.
Доказательство. Заметим, что разложение (5.1): определителя по какой-либо i-й строке совпадает с разложением определителя транспонированной матрицы по i-му столбцу.
2. При перестановке местами двух строк определителя последний меняет знак на противоположный.
Доказательство.
Для определителя
это свойство проверяется элементарно.
Для
запишем формулу Лапласа разложения по
строкам
и
:
.
При перестановке
местами строк
и
определители второго порядка
меняют знак, а остальные величины в
выражении для
не зависят от элементов строк
и
,
поэтому сохраняют свое значение.
3. Определитель с двумя одинаковыми строками равен нулю.
Доказательство. При перестановке двух одинаковых строк определитель не должен измениться, а с другой стороны, по свойству 2 он должен изменить знак на противоположный. Поэтому имеет место равенство = - . Откуда 2 = 0 или = 0.
4.
Умножение числа
на определитель
эквивалентно умножению на число
всех элементов какой-либо строки.
Другими словами, общий множитель всех элементов какой-либо строки определителя можно выносить за знак этого определителя.
Доказательство. Разложим определитель по элементам какой-либо i-й строки. Тогда, при умножении числа на каждый элемент этой строки умножится на . Соберем определитель к первоначальному виду, получим определитель, каждый элемент i-й строки умножится на число .
Продемонстрируем доказательство на примере
.
5. Если все элементы какой-либо строки определителя равны нулю, то определитель равен нулю.
Доказательство. В предыдущем свойстве достаточно положить =0.
6. Если элементы каких-либо двух строк определителя пропорциональны, то он равен нулю.
Доказательство. Вынося множитель пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который равен нулю по свойству 3.
7. Если каждый элемент какой-либо строки определителя представляет сумму двух слагаемых, то он может быть представлен в виде суммы двух определителей:
.
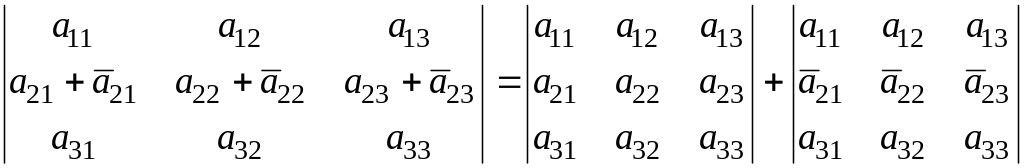Доказательство. Достаточно разложить исходный определитель по элементам второй строки, а затем собрать в виде суммы двух определителей, как это делалось при доказательстве свойства 4.
8. Величина определителя не изменится, если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженной на произвольный множитель :
.
Доказательство. Разложим полученный определитель на сумму двух определителей по свойству 7. Получим исходный определитель и определитель с двумя пропорциональными строками, который по свойству 6 равен нулю.
9. Сумма произведений элементов какой-либо строки определителя на соответствующие алгебраические дополнения элементов этой строки (какой-либо другой стоки) равна величине этого определителя (равна нулю):
Доказательство.
Первое утверждение при i=k
является
определением определителя
,
а второе следует из того, что при
имеем определитель с двумя одинаковыми
строками.
Пример 1.
Вычислим определитель
:
.
Сначала вычтем из 1-го столбца (а) утроенный 4-й столбец, получим (б). Вычислим (б), разлагая определитель по элементам 1-го столбца, получим (в). Затем, из 2-го столбца вычтем удвоенный 1-й столбец, получим (г). Вычислим (г), разлагая определитель по элементам 1-й строки, получим (д). Вычислим (д), получим 800.
Пример 2. Вычислим так называемый определитель Вандермонда
.
Для этого вычтем 1-й столбец из всех последующих, начиная со второго, и полученный определитель разложим по элементам первого столбца, т.е.
.
Теперь, вычтем из
каждой строки предыдущую, умноженную
на
и вынесем общие множители из всех n
столбцов за знак определителя, т.е.
.
Поступая
аналогично с определителем
,
получим
.
Продолжая процесс, окончательно имеем
.