Заочный факультет «Высшая математика» Мироненко Л.П., Локтионов И.К.
ЛИНЕЙНАЯ АЛГЕБРА
1. Матрицы и определители
1.1. Понятие числовой матрицы
Определение. Числовой матрицей А размерности m ´ n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.
Обозначают матрицы так:
.
Вместо круглых
скобок в литературе также используют
квадратные
,
двойные прямые
.
Числа m
и n
называют порядками матрицы. В частности,
при m = n
матрица называется квадратной порядка
n.
Числа
,
составляющие матрицу, называются ее
элементами, при этом индекс i
обозначает номер строки, j
- номер столбца на пересечении которых
стоит элемент
.
Примеры числовых матриц:
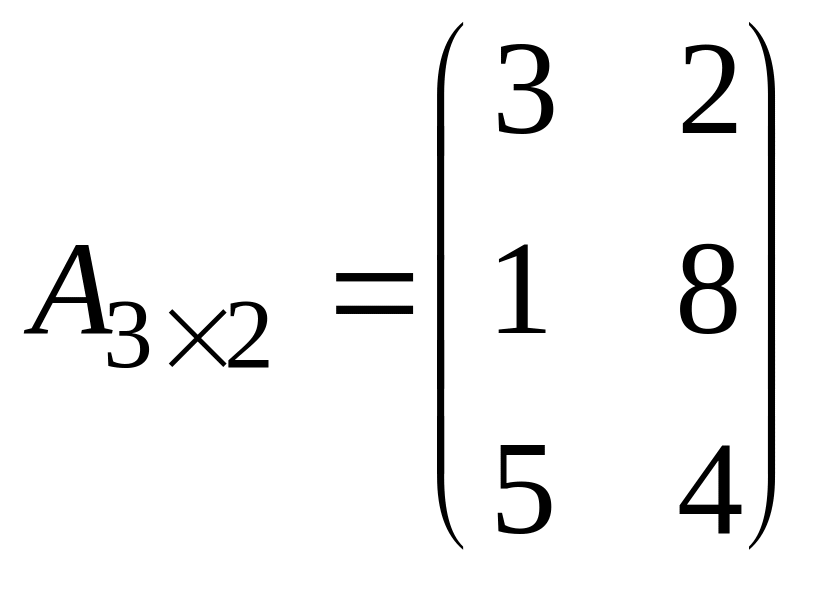- матрица размерности
3 х 2;
- матрица-строка;
- матрица-столбец;
- квадратная
матрица второго порядка.
В случае квадратной матрицы
вводят понятия
главной и побочной диагоналей. Главную
диагональ матрицы образуют элементы
,
побочную - элементы
.
По внешнему виду квадратные матрицы подразделяют:
а)
треугольные - матрицы у которых
при
или
при
,
т.е.
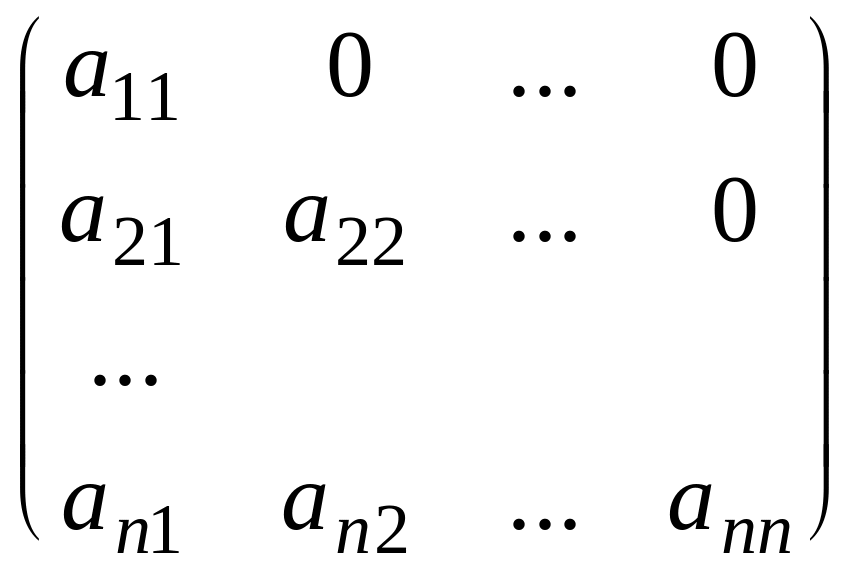или
;
б)
строго треугольные - треугольные матрицы
у которых элементы главной диагонали
равны нулю
.
в)
диагональные - матрицы у которых
при
,т.е.
;
г)
единичная - диагональная матрица у
которой
,
т.е.
;
д) нулевая - матрица, все элементы которой равны нулю
;
е) мономиальные - матрицы у которых в каждой строке и в каждом столбце имеется лишь один элемент, отличный от нуля. Например, единичная матрица Е является мономиальной.
1.2. Операции над матрицами и их свойства
Матрицы
и
называются равными
,
если они одних порядков m
и n
и
.
Обозначают: .
а)
СЛОЖЕНИЕ МАТРИЦ. Суммой
матриц
и
(одинаковых порядков
m
и n)
называется той же размерности m
´
n матрица
,
элементы которой находятся по формуле
.
Обозначают:
.
Пример 1.
Найдем сумму матриц
и
.
Согласно правилу (а)
.
Свойства операции сложения:
1.
коммутативность
;
2.
ассоциативность
;
3.
свойство нулевой матрицы
.
б)
УМНОЖЕНИЕ ЧИСЛА НА МАТРИЦУ.
Произведением
числа l
на матрицу
(порядков m
и n)называется
той же размерности матрица
,
элементы которой находятся по формуле
.
Обозначают:
.
Пример 2.
Найдем произведение числа
на матрицу
.
Согласно правилу (б) имеем
.
Свойства операции умножения числа на матрицу:
4.
ассоциативность
;
5.
дистрибутивность относительно суммы
матриц
;
6.
дистрибутивность относительно суммы
чисел
;
7.
особая роль числового множителя 1:
;
Введем понятие
противоположной матрицы
данной матрице
соотношением
.
Тогда имеет место еще одно свойство
8.
свойство противоположной матрицы
.
Определение. Множество R элементов А,В,С,... любой природы называется линейным (афинным) пространством, если для его элементов определены операции сложения (а) и умножения на число (б) и эти операции удовлетворяют аксиомам линейности 1-8.
Примеры линейных пространств:
множество вещественных чисел R;
множество векторов A;
множество матриц A одних и тех же порядков m и n.
в)
УМНОЖЕНИЕ МАТРИЦ. Произведением
матриц
и
размерностей m
´
n
и n
´
p
соответственно называется матрица
размерности m
´
p,
элементы которой вычисляются по формуле
Обозначают:
.
Для запоминания
пользуются
правилом:
элемент
матрицы
равен сумме попарных произведений
элементов
й
строки матрицы А
и
го
столбца матрицы
.
Замечание 1. Матрицу А можно умножить не на всякую матрицу В - необходимо, чтобы число столбцов матрицы А было равно числу строк матрицы В. В частности, оба произведения АВ и ВА существуют, если обе матрицы квадратные и одинаковых порядков.
Пример 3.
Найдем произведение матриц
и
.
Согласно правилу
(в) имеем
.
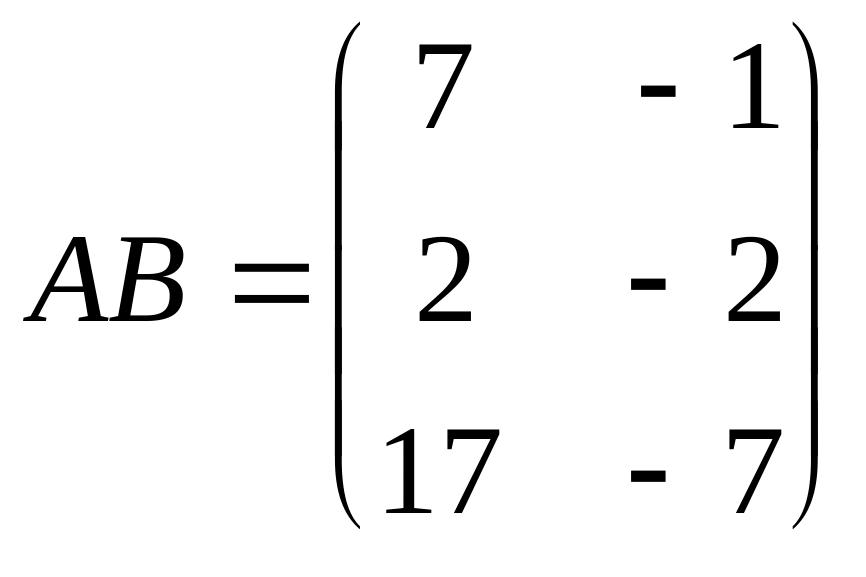Заметим, что
произведение
не существует.
Замечание 2
Легко убедиться в том, что в общем случае
произведение матриц не коммутативно,
т.е.
.
Это характерное свойство матриц.
Свойства произведения матриц:
1.
ассоциативность
;
2.
дистрибутивность
;
3.
свойство единичной матрицы
.
г)
ТРАНСПОНИРОВАНИЕ МАТРИЦЫ.
Матрица
называется транспонированной, если она
получается из матрицы А
переменой местами строк и столбцов,
т.е. если
,
то
.
Пример 4.
Транспонируем матрицу
.
Согласно правилу (г) имеем
.
Свойства операции транспонирования:
1.
;
2.
;
3.
;
4.
;
5.
.