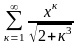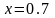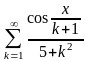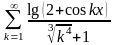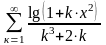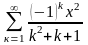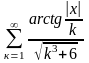Приклад виконання завдання 3
Схема алгоритму має циклічну структуру і представлена на рис. 3
Рис.3. Схема алгоритму циклічної
структури
Побудова графіку функції y(x).
Рис.4. Графік функції y(x)
Для форматуванням графіку, необхідно двічі по ньому клацнути лівою кнопкою миші. У вікні форматування графіку перейти на закладку Traces.
Пропонується змінити колір, тип і товщину лінії.
Завдання 4
Організація ітераційного циклу.
В ітераційних циклах число повторень залежить від виконання умови.
Обчислити суму ряду S(x) з точністю = 10-5
Вивести величину суми ряду S , число членів ряду k, необхідних при додаванні для досягнення заданої точності .
|
Сумма ряда |
х |
|
|
Сумма ряда |
х |
1 |
|
|
|
11 |
|
х =1.7 |
2 |
|
|
|
12 |
|
х = 0.8 |
3 |
|
|
|
13 |
|
х =3,8
|
4 |
|
|
|
14
|
|
х =5,1
|
5 |
|
|
|
15
|
|
х = 2,3
|
6 |
|
|
|
16
|
|
х = 0,9
|
7 |
|
|
|
17
|
|
х = 0,8
|
8 |
|
|
|
18
|
|
х = 1,3
|
9 |
|
|
|
19
|
|
х =1,8
|
10 |
|
|
|
20 |
|
х = 0,7 |
21 |
|
х = 3.4 |
|
22 |
|
х =5,8
|
23 |
|
х =2,8
|
|
24 |
|
х =3,1
|
25
|
|
х =3,1
|
|
26 |
|
х = 1,3
|
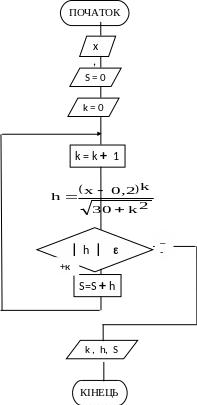
Рис.10. Схема алгоритму пошуку суми ряду
Програма
Перевірка
Завдання 5 Рішення нелінійних рівнянь
1. Розв'язати нелінійне рівняння за допомогою функції root.
2. Побудувати графік функції.
3. Із графіку виявити кількість коренів і призначити початкові значення для отримання результатів рішення рівняння.
4. Відмітити на графіку точки перетину з віссю, як показано на рис.
.
Варіант |
Рівняння |
|
Варіант |
Рівняння |
1 |
f(x) = x2 – 3,5 |
|
14 |
f(x) = - ( x + 1 )3 + 11х |
2 |
f(x) = x2 - 12 |
|
15 |
f(x) = - ( x - 1)2 + 4,5 |
3 |
f(x) = -x2 + 13 |
|
16 |
f(x) = ex – (x3 – 2) |
4 |
f(x) = - x2 + 5 |
|
17 |
f(x) = 3( x – 0,5 )2 – 6. |
5 |
f(x) = ex – (x3 – 2) |
|
18 |
f(x) = - x2 +3х -1 |
6 |
f(x) = 5x2 - ex-12 |
|
19 |
f(x) = x3 – 4 x - 2 |
7 |
f(x) = (x+2)2 - ex-5 |
|
20 |
f(x) = - x3 + 1.5 x +0,5 |
8 |
f(x) = 0,5(x-2)2 - 3 |
|
21 |
f(x) = - x3 +15x-5 |
9 |
f(x) =(0,5 x-1)2 - 2 |
|
22 |
f(x) = x2 – 3х -3 |
10 |
f(x) = - x3 +12х |
|
23 |
f(x) = - 4x3 + 14 х - 4 |
11 |
f(x) = x3 – 17(х-1) |
|
24 |
f(x) = - 5x3 +15 x - 5 |
12 |
f(x) = - x3 – 10 (х-0,5) |
|
25 |
f(x) = x3 + x2 – 0,1 |
13 |
f(x) = - (x – 1 )2 + 12 |
|
26 |
f(x) = -x3 + 25х - 25 |