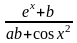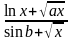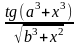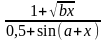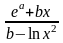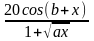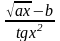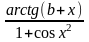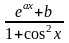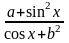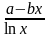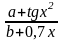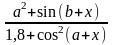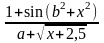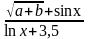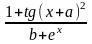Приклад виконання
Обчислити функцію y(x) для кожного значення аргументу x1, x2, x3 , де a = cos 3,5 , b = arctg 9
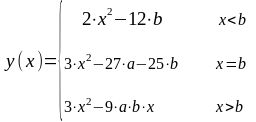
Значення x1, x2, x3 задати самостійно відносно до величини b. Усі розрахунки виконати з точністю до трьох значущих цифр (використати функцію round). Скласти схему алгоритму.
Схема алгоритму має розгалужену структуру і представлена на рис. 2.
ПОЧАТОК
a = cos 3,5
a
b = arctg 9
b
x <b
x =b
x1 , x2 , x3
y(x3)
КІНЕЦЬ
y(x1)
y(x)=
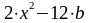
y(x2)
y(x)=
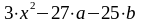
y(x)=
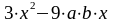
Рис.2. Схема
алгоритму розгалуженої структури
Спочатку обчислюються величини а і b . Так як, по умові завдання x порівнюється з b , результат обчислення b округлюється до трьох значущих цифр, використовуючи функцію round.
Щоб перевірити виконання розрахунку функції y(x) по трьом гілкам розгалуженого процесу, значення x1, x2, x3 задаються самостійно, відносно до величини b. Наприклад, x1 задається меншим за b , x2 рівним b і x3 більшим за b.
Виведемо результати обчислень по трьом гілкам розгалуженого процесу.
При умовах x < b , x = b і x < b
Завдання 3
Організація алгоритмів циклічної структури Арифметичний цикл.
Алгоритм циклічної структури – це такий алгоритм, в якому одні й ті ж дії повторюються багаторазово, в залежності від початкових даних або проміжних результатів.
В арифметичних циклах число повторень наперед відоме.
Скласти схему алгоритму та програму для обчислення відповідної кожному варіанту функції y( x ). Аргумент x змінюється від xf до xe з кроком x. Початкові дані і результати вивести у вигляді таблиць значень x і y(x).
Побудувати графік функції , якщо він ма вигляд ламаної лінії. Яке початкове значення потрібно змінити, що графік функції не? Самостійно задати інтервал для побудови графіка функції. Побудувати графік функції.
На отриманому графіку показати значення функції Y(d) (величину d задати самостійно)
Варіант |
а |
b |
x поч |
x кін |
x |
y(x) |
1 |
0,2 |
3,45 |
24 |
26 |
0,1 |
|
2 |
2,3 |
0,55 |
11 |
20 |
2,2 |
|
3 |
1,4 |
1,65 |
12 |
16 |
0.5 |
|
4 |
3,5 |
0,75 |
13,5 |
17 |
0,4 |
|
5 |
1,6 |
3,85 |
15 |
30 |
2,5 |
|
6 |
1,7 |
0,95 |
15 |
25 |
1.5 |
|
7 |
1,8 |
3,5 |
2 |
10 |
1,3 |
|
8 |
1,9 |
0,2 |
-10 |
10 |
2.5 |
|
9 |
1,15 |
2,3 |
4 |
12 |
0.7 |
|
10 |
1,25 |
2,4 |
1.1 |
10 |
0,8 |
|
11 |
1,35 |
3,5 |
5 |
10 |
1,25 |
|
12 |
1,45 |
1,6 |
6 |
8 |
0,35 |
|
13 |
1,55 |
1,7 |
20 |
30 |
1,45 |
|
14 |
1,65 |
1,8 |
4 |
10 |
0,8 |
|
15 |
0,1 |
0,2 |
10 |
18 |
0,5 |
|
16 |
1,2 |
2,3 |
4 |
12 |
0,75 |
|
17 |
2,3 |
1,4 |
2 |
15 |
1,5 |
|
18 |
0,4 |
3,5 |
25 |
35 |
0,95 |
|
19 |
1,5 |
1,6 |
30 |
46 |
1,1 |
|
20 |
0,6 |
1,7 |
31 |
47 |
0,8 |
|
21 |
2,7 |
1,8 |
1 |
16 |
1.5 |
|
22 |
0,8 |
1,9 |
3 |
10 |
1,4 |
|
23 |
1,9 |
0,1 |
1 |
15 |
1,5 |
|
24 |
0,15 |
1,2 |
2 |
16 |
1,6 |
|
