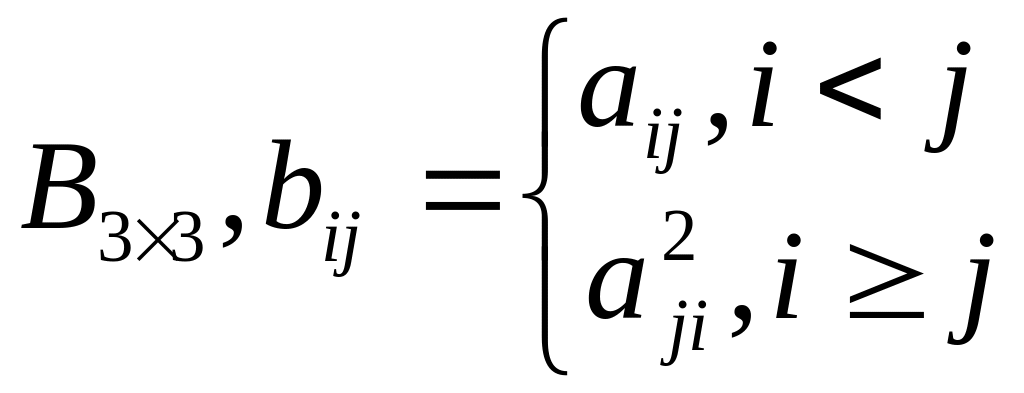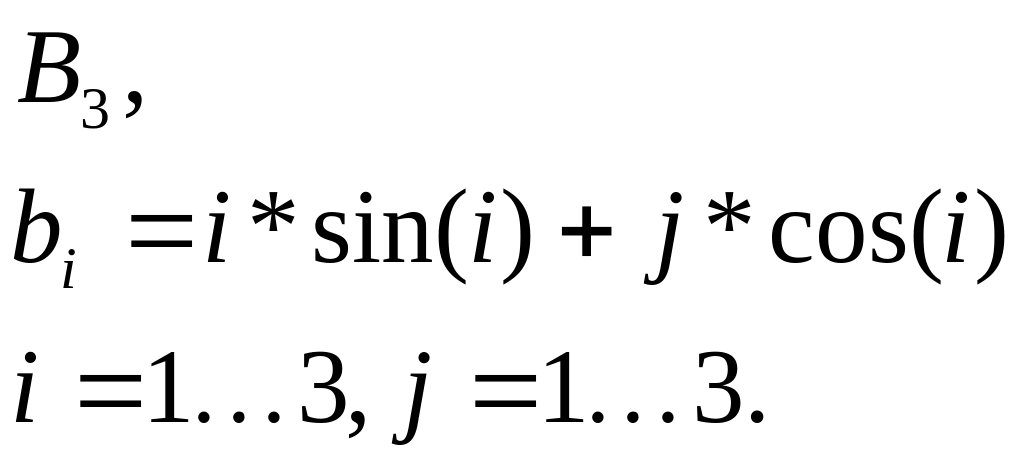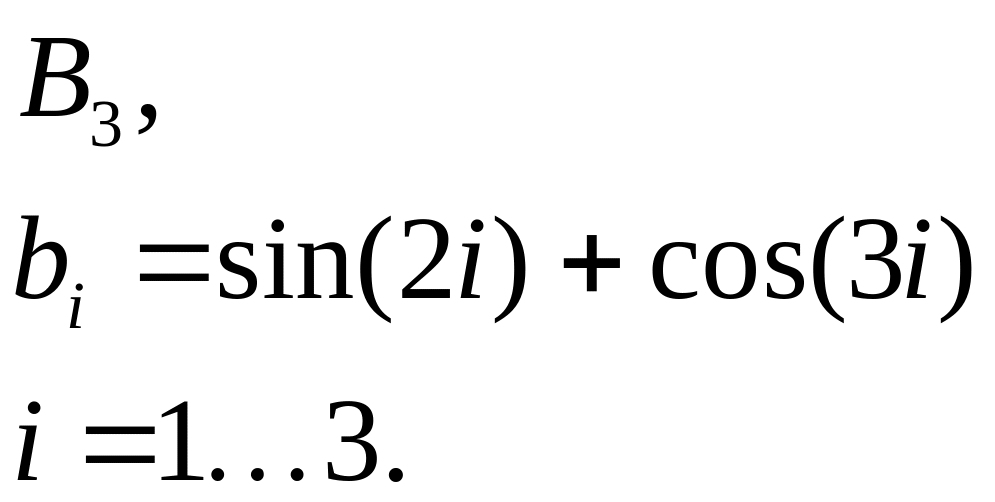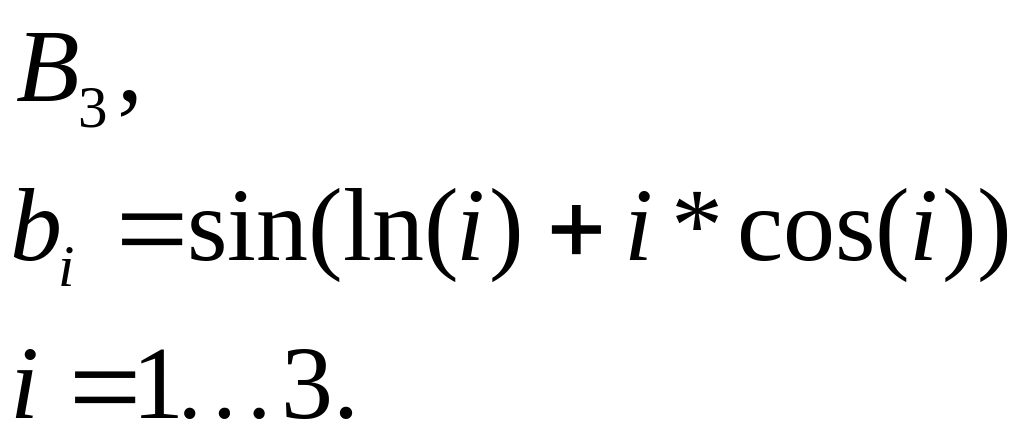Файл-функции

Файл-функции выполняют необходимые действия с входными аргументами и возвращают результат в выходных аргументах. Идентификация файла как функции выполняется установкой слова function в первой строке, т.е. заголовке функции:

Структура такого модуля с одним выходным параметром выглядит следующим образом:

function var = f_name(Cпиcoк_napaмeтpов) 

%Основной комментарий

%Дополнительный комментарий 

Тело файла с любыми выражениями 

vаr=выражение

Например,

function f = myfun(x)

f = exp(-x) * sqrt((x^2 + 1) / (x^4 + 0.1));

В заголовке функции также размещаются имя функции и списки входных и выходных аргументов. Входные аргументы записываются в круглых скобках после имени функции (в примере – это x). Выходной аргумент указывается слева от знака равенства в заголовке функции (в примере – это f).

После заголовка размещается тело файл-функции – один или несколько операторов.

Использовать файл-функцию можно так же, как и встроенные функции, например

>> y = myfun(1.3)

y =

0.2600

Каталог, в котором содержатся файл-функции, должен быть текущим, или путь к нему должен быть добавлен в пути поиска.

Использование файл-функций упрощает визуализацию результатов математических действий. Например, требуется определить значение функции myfun на отрезке [0, 4]. Из командной строки это выглядит следующим образом (результат выполнения показан на рис. 3.3):

>> x = 0 : 0.5 : 4;

>> y = myfun(x);

>> plot(x, y)

Рисунок 3.3– Пример использования plot

Но аналогичную задачу можно решить при помощи функции fplot, которой требуется указать имя файл-функции myfun или указать на нее (с оператором @ перед именем функции) и границы отрезка для построения графика:

>> fplot('myfun', [0 4]) или >> fplot(@myfun, [0 4]).

Результат выполнения показан на рис. 3.4.

Рисунок 3.4 – Пример использования fplot

График, построенный fplot, более точно отражает поведение функции, так как алгоритм автоматически подбирает шаг аргумента, уменьшая его на участках быстрого изменения исследуемой функции.

Если функция имеет несколько входных аргументов, то они размещаются в списке через запятую.

Если список выходных аргументов пуст, то файл-функция не будет возвращать никаких значений.

Если функция имеет несколько выходных аргументов (вектор-функция), то они добавляются через запятую в список выходных аргументов. Например, файл-функция для перевода времени, заданного в секундах, в часы, минуты и секунды:

function [hour, minute, second] = hms(sec)

hour = floor(sec/3600);

minute = floor((sec – hour*3600)/60);

second = sec – hour*3600 – minute*60;

При вызове файл-функции с несколькими выходными аргументами результат следует записывать в вектор соответствующий длины:

>> [H, M, S] = hms(10000)

H =

2

M =

46

S =

40

Файл-функции можно сопроводить комментариями. Все комментарии после заголовка и до тела функции или пустой строки выводятся в командное окно по команде help. Например:

function [hour, minute, second] = hms(sec)

% hms – перевод секунд в часы, минуты и секунды

% [hour, minute, second] = hms(sec)

% sec – число секунд

% hour – число полных часов

% minute – число полных минут

% second – остаток секунд

hour = floor(sec/3600);

minute = floor((sec – hour*3600)/60);

second = sec – hour*3600 – minute*60;

Первая строка комментариев после заголовка функции называется H1-line и используется при поиске командой lookfor. Эта команда ищет указанное слово в строках H1-line всех файл-функций в каталогах, указанных в путях поиска, в том числе, и в текущем каталоге.

Для организации диалогового ввода и вывода используются следующие операторы, представленные в табл. 3.1.

Таблица 3.1 – Операторы диалогового ввода/вывода

Оператор	Синтаксис	Назначение
INPUT	x = input(‘<приглашение>’)	Для ввода данных с клавиатуры
DISP	disp (<переменная или текст в апострофах>)	Для вывода на дисплей

Приведем простой пример диалоговой программы, которая служит для многократного вычисления длины окружности по вводимому пользователем значению радиуса r (рис. 3.5).

Рисунок 3.5 – Пример диалоговой программы

Для организации ветвлений служат условные операторы.

Конструкции условных операторов:

1) if <условие>

<операторы>

end

Операторы (тело выражения) выполняются только в том случае, если условие истинно, если условие ложно, то тело выражения не выполняется.

2) if <условие>

<операторы 1>

else

<операторы 2>

end

Если ход программы должен изменяться в зависимости от нескольких условий, то следует использовать полную конструкцию if-elseif-else. Каждая из ветвей elseif в этом случае должна содержать условие выполнения блока операторов, размещенных после нее. Важно понимать, что условия проверяются подряд, первое выполненное условие приводит к работе соответствующего блока, выходу из конструкции if-elseif-else и переходу к оператору, следующему за end. У последней ветви else не должно быть никакого условия. Операторы, находящиеся между else и end, работают в том случае, если все условия оказались невыполненными.

Например, требуется написать файл-функцию для вычисления кусочно-заданной функции (рис. 3.6).

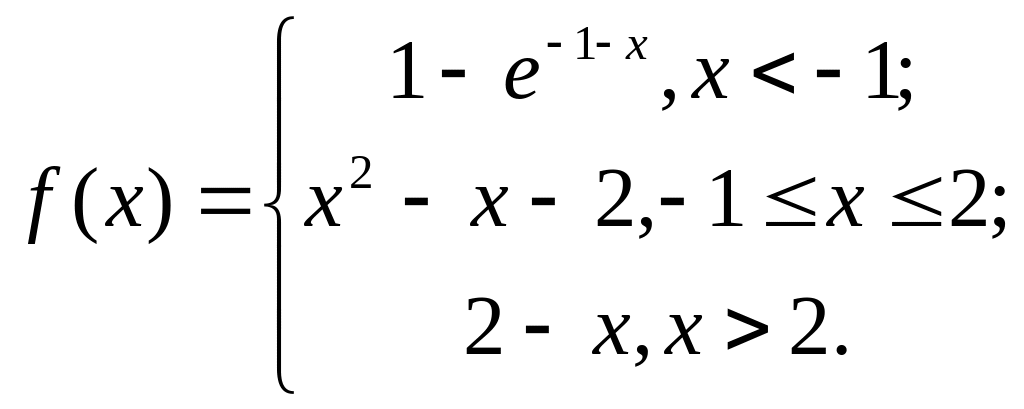
Рисунок 3.6 – Листинг программы для вычисления значения функции

В системе MatLab могут применяться следующие операторы сравнения, приведенные в табл. 3.2.

Таблица 3.2 – Операторы сравнения

Символ	Назначение	Имя функции
<	Меньше	lt
>=	Больше или равно	ge
>	Больше	gt
<=	Меньше или равно	le
= =	Равно	eq
~=	Не равно	ne

Операции (= =, ~=) проводят сравнение вещественных и мнимых частей комплексных чисел, а операции (>, <, >=, <=) – только вещественных частей.

Логические операции можно записывать в виде функций (табл. 3.3).

Таблица 3.3 – Логические операции

Символ	Назначение	Имя функции
&	Логическое «и»	and
|	Логическое «или»	or
~	Отрицание	not

Результатом логических операций являются числа 0 (false) и 1(true).

В системе MatLab есть две разновидности операторов цикла – условный и арифметический. Для повторения операторов нефиксированное число раз используется оператор цикла с предусловием: Оператор цикла while

while <условие>

<операторы>

end

Операторы выполняются, если переменная <условие> имеет ненулевые элементы.

Рассмотрим пример на вычисление суммы, похожий на пример из предыдущего пункта. Требуется найти сумму ряда для заданного x (разложение в ряд sin(x)):

.

Сумму можно накапливать до тех пор, пока слагаемые являются не слишком маленькими, скажем больше по модулю 10^-10. Решаем задачу с применением цикла  while,  который работает, пока выполняется условие цикла:

while  условие цикла команды MatLab end

Листинг файл-функции  mysin, вычисляющей синус разложением в ряд:

function S = mysin(x) % Вычисление синуса разложением в ряд % Использование: y = mysin(x), -pi<x<pi

S = 0;

k = 0;

while abs(x.^(2*k+1)/factorial(2*k+1))>1.0e-10

S = S + (-1)^k*x.^(2*k+1)/factorial(2*k+1);

k = k + 1;

end

Арифметический оператор цикла имеет следующий вид:

for <имя> = <НЗ>: <Шаг>: <КЗ>

<операторы>

end,

где <имя> – имя управляющей переменной цикла;

<НЗ> – начальное значение управляющей переменной;

<КЗ> – конечное значение управляющей переменной;

<Шаг> – приращение значений переменной <имя> в ходе ее изменения от значения <НЗ> до значения <КЗ>. Если параметр <Шаг> не указан, по умолчанию его значение принимается равным единице.

При работе с циклом for допустимо использование оператора прерывания цикла break. При работе данного оператора работа цикла завершается, и управление передается на следующий после конца цикла оператор.

Пример 1 – программа с циклами:

сlear

x1=1:0.01:pi;

y1=sin(x1);

k=3;

x=1:0.01:pi

n=length(x);

n

slag=1;

y2=1;

for i=2:k

slag=slag.*(-x.^2)./((2.*i-2)*(2.*i-1));

y2=y2+slag;

end;

y2

[x' y1' y2']

plot(x1,y1,'r')

hold on

plot(x,y2,'g:')

Рисунок 3.7 – Результат работы прогаммы 1

Пример 2 – программа с циклами:

clear

x1=1:0.01:pi;

y1=sin(x1);

k=3;

x=1:0.1:pi;

n=length(x);

n

for m=1:n

slag(m)=x(m);

y2(m)=x(m);

for i=2:k

slag(m)=slag(m).*(-x(m).^2)./((2.*i-2)*(2.*i-1));

y2(m)=y2(m)+slag(m);

end;

end;

n2=length(y2);

n2

y2;

[x' y2']

plot(x1,y1,'r')

hold on

plot(x,y2,'g:')

hold off

Рисунок 3.8 – Результат работы прогаммы 2

Пример 3:Напишите файл-программу для вычисления суммы

Алгоритм вычисления суммы использует накопление результата, т.е. сначала сумма равна нулю (S = 0), затем в переменную k заносится единица, вычисляется 1/k!, добавляется к S  и результат снова заносится в S. Далее k увеличивается на единицу, и процесс продолжается, пока последним слагаемым не станет 1/10!. Файл-программа  Prim3, приведенная в следующем листинге, вычисляет искомую сумму.

Листинг файл-программы Prim3 для вычисления суммы:

% файл-программа для вычисления суммы % 1/1!+1/2!+ … +1/10!

% Обнуление S для накопления суммы S = 0; % накопление суммы в цикле for k = 1:10 S = S + 1/factorial(k); End % вывод результата в командное окно S

Набрать файл-программу в редакторе М-файлов, сохранить её в текущем каталоге в файле  Prim3.m  и выполнить. Результат отобразится в командном окне, так как в последней строке файл–программы  S  содержится без точки с запятой для вывода значения переменной S.

S = 1.7183

Пример 4: табулирование с условием, дифференцирование и интегрирование

Листинг файл-программы:

clear

x=0:0.05:4;

a=x<=2;

for i=1:length(a)

if a(i)

y(i)=x(i);

else y(i)=3.*x(i);

end;

end;

[x' y']

figure(1)

plot(x,y,'r') % вывод графика функции

s=trapz(x,y)

s2=quad(@funs,0,4,1e-4)

figure(2)

f1=diff(funs(x));

x1=x(1:end-1)

plot(x1,f1) % вывод графика производной

Рисунок 3.9 – График функции

Рисунок 3.10 – График производной

Ход работы программы может определяться значением некоторой переменной (переключателя) т.е. способ ветвления программы основан на использовании оператора переключения switch. Оператор switch содержит блоки, начинающиеся со слова case, после каждого case записывается через пробел, то значение переключателя, при котором выполняется данный блок. Последний блок начинается со слова otherwise, его операторы работают в том случае, когда ни один из блоков case не был выполнен. Если хотя бы один из блоков case выполнен, то происходит выход из оператора switсh и переход к оператору, следующему за end.

Предположим, что требуется найти количество единиц и минус единиц в заданном массиве и, кроме того, найти сумму всех элементов, отличных от единицы и минус единицы. Листинг программы содержит файл–функцию, которая по заданному массиву возвращает число минус единиц в первом выходном аргументе, число единиц – во втором, а сумму – в третьем (рис.3.11).

Рисунок 3.11 – Листинг программы

Для остановки программы используется оператор pause. Он используется в следующих формах:

1. pause — останавливает вычисления до нажатия любой клавиши; 

2. pause(N) — останавливает вычисления на N секунд; 

3. pause on — включает режим отработки пауз; 

d) pause off — выключает режим отработки пауз. 

Оператор прерывания цикла break

При организации циклических вычислений следует заботиться о том, чтобы внутри цикла не возникло ошибок. Например, пусть задан массив x, состоящий из целых чисел, и требуется сформировать новый массив y по правилу  y(i) = x(i+1)/x(i).  Очевидно, что задача может быть решена при помощи цикла  for. Но если один из элементов исходного массива равен нулю, то при делении получится  inf,  и последующие вычисления могут оказаться бесполезными. Предотвратить эту ситуацию можно выходом из цикла, если текущее значение  x(i)  равно нулю. Следующий фрагмент программы демонстрирует использование оператора  break  для прерывания цикла:

for x = 1:20 z = x-8;  if z==0 break end y = x/z end

Как только переменная z принимает значение 0, цикл прерывается.

Оператор  break  позволяет досрочно прервать выполнение циклов for и while. Вне этих циклов оператор  break  не работает.

Если оператор  break  применяется во вложенном цикле, то он осуществляет выход только из внутреннего цикла.

Лабораторная работа № 3

ПРОГРАММИРОВАНИЕ В СРЕДЕ MATLAB

Цель работы: ознакомиться с операциями отношения, логическими операциями и условными операторами, приобрести навыки их использования при разветвленных и циклических вычислениях.

Контрольные вопросы

1. Как осуществляется диалоговый ввод и вывод?

2. Для чего используются условные операторы?

3. Чем отличаются файлы-сценарии от файлов?.

4. Как осуществляется диалоговый ввод и вывод?

5. Для чего используются условные операторы?

6. Чем отличаются файлы-сценарии от файлов-функций?

Лабораторное задание

1. Из файла-сценария с помощью функции диалогового ввода ввести с клавиатуры все необходимые данные. Выполнить расчет с использованием условных операторов и вывести результаты в командное окно (табл. 3.1).

Таблица 3.1 − Варианты заданий

№ варианта	Задание
1	Найти сумму положительных из четырех заданных переменных.
2	Найти максимальное значение из четырех заданных переменных и вывести ее
3	Заданы четыре переменные. Наименьшую из них заменить на сумму остальных
4	Заданы четыре переменные. Подсчитать количество отрицательных и количество нулевых из них
5	Найти произведение отрицательных из четырех заданных переменных
6	Заданы две фигуры: квадрат задан длиной стороны, а круг – длиной радиуса. Определить, какая из них имеет большую площадь и во сколько
7	Заданы четыре переменные. Все отрицательные из них заменить абсолютными значениями и увеличить в 2 раза
8	Заданы четыре переменные, подсчитать количество равных нулю, положительных и отрицательных
9	Даны четыре переменные. Найти среди них переменные, наиболее близкие по значению к
10	Заданы четыре переменные. Все положительные из них заменить отрицательными значениями, умноженными на 5
11	Найти минимальное и максимальное значения из четырех заданных переменных
12	Заданы четыре значения. Определить какие из них целые
13	Заданы четыре переменные. Подсчитать количество и произведение значений, попавших в интервал [1 5].
14	Заданы четыре переменные. Подсчитать количество отрицательных и количество нулевых из них.
15	Найти произведение отрицательных из четырех заданных переменных

2. Написать файл-функцию с использованием операторов ветвления и циклов, на основании вариантов задания, представленных в табл.3.2.

Таблица 3.2 – Варианты заданий

№	Вход. массив	Формируемый массив	Задача
1			Сформировать массив А1 из минимальных элементов строк матрицы А и массив В1 из минимальных элементов строк матрицы В. Среди элементов А1 и В1 найти максимальный
2			Сформировать массив С – сумму элементов массивов А и В. Найти максимальное значение массивов А, В, С.
3			Определить минимальные элементы в матрицах А и В (mА и mВ). Вычислить С=А*В*mА*mВ
4			Сформировать массив А1 из максимальных элементов строк матрицы А и массив В1 из максимальных элементов строк матрицы В. Упорядочить массив А1 по возрастанию, а массив В1 – по убыванию
5			Определить максимальные элементы в матрице А и массиве В (mА и mВ). Вычислить С=А*В*mА*mВ
6			Сформировать массив А1 из средних значений элементов строк матрицы А. Упорядочить массив А1 по возрастанию, а В – по убыванию. Осуществить поэлементное умножение А1 и В
7			Заменить строку матрицы А, содержащую максимальный элемент, массивом В. Вычислить сумму элементов полученной матрицы
8			Массив А упорядочить по возрастанию и заменить им последнюю строку матрицы В
9			Упорядочить по возрастанию массивы А и В. Осуществить поэлементное деление упорядоченных массивов. Определить произведение элементов результирующего массива
10			Вычислить произведение элементов матрицы А (рА) и сумму элементов матрицы В (сВ). Вычислить матрицу С=рА*сВ*А*В'
11			Определить минимальные элементы в матрицах А и В (mА и mВ). Вычислить С=А*В*mА*mВ
12			Сформировать массив А1 из максимальных элементов строк матрицы А. Осуществить поэлементное умножение А1*В. Упорядочить массив А1 по возрастанию
13			Заменить строку матрицы А, содержащую минимальный элемент, массивом В. Вычислить произведение элементов полученной матрицы
14			Массив А упорядочить по убыванию и заменить им первую строку матрицы В
15			Сформировать массив С – произведение элементов массивов А и В. Найти максимальные и минимальные значения массивов А, В, С
16			Вычислить сумму элементов матрицы А (рА) и произведение элементов матрицы В (сВ)
17			Вычислить произведение элементов матрицы А (рА) и сумму элементов матрицы В (сВ).