Дифференциальные уравнения и системы уравнений

Необходимо решить уравнение:

Попробуем решить его с помощью программы Simulink пакета MatLab.

Нам необходимо создать схему уравнения, для этого создадим обратную связь между выходными значениями интегратора и новым значением переменной. У нашего уравнения линейно изменяется x от 0 до 20. Поэтому для решения уравнения необходимо использовать блок Ramp. В конце обязательно должен быть интегрирующий блок, а из него результат выходит на осциллограф (рис. 7.22).

Рисунок 7.22 – Метод решения дифференциальных уравнений

Решение уравнения выглядит как показано на рис. 7.23. Результатом будет график x от y:

Рисунок 7.23 – Результат решения дифференциальных уравнений

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources. Формирует линейный сигнал. В параметрах необходимо задать 1.

Add – Math Operations. В параметрах выбираем необходимые нам операции.

Gain – Math Operations. Коэффициент усиления сигнала. В параметрах ставим значение 3/2.

Sine Wave Function – Sources. Т.к. нам необходим косинус, то в параметрах Phase ставим pi/2.

Integrator – Continuous. Выполняет интегрирование входного сигнала.

Scope – Sinks. Выводим результат – график сигнала в функции времени.

Дифференциальные уравнения 2-го порядка.

Дана система уравнений:

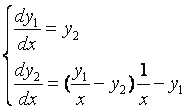
Решим ее с помощью программы Simulink пакета MatLab. Решаем аналогично предыдущему случаю.

Рисунок 7.24 – Метод решения дифференциальных уравнений 2-го порядка

В данной системе уравнений линейно изменяется x от 1 до 10. Также необходимо сделать обратную связь между выходными значениями интеграторов и новым значение переменной x. Обязательно надо в интеграторах задать начальные значения y₁(0) = 0.1; y₂(0) = 0.5.

Рисунок 7.25 – Результатом будут два графика

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources. Формирует линейный сигнал. В параметрах необходимо задать все значения 1.

Integrator – Continuous. Выполняет интегрирование входного сигнала. Необходимо задать начальные значения Initial condition для y₁ 0.1, для y₂ 0.5.

Add – Math Operations. В параметрах выбираем необходимые нам операции.

Divide - Math Operations. Деление первой входной величины на вторую.

Dot Product - Math Operations. Перемножение.

Scope – Sinks. Выводим результат – график сигнала в функции времени.

Лабораторная работа №7

Основные возможности пакета математического моделирования Simulink

Цель работы: ознакомиться с возможностями пакета математического моделирования Simulink

Контрольные вопросы

1. Из каких библиотек состоит пакет Simulink?

2. Как собрать модель в пакете Simulink?

3. Как изменить параметры моделирования?

4. Какие существуют способы визуализации процесса моделирования?

Лабораторное задание

1.Ознакомиться со структурой иерархической библиотеки Simulink.

2. Набрать модель системы, выданную преподавателем.

3. Произвести моделирование системы.

4. Сравнить результаты, полученные путем изменения параметров моделирования.

5. Представить схему модели и результаты моделирования.

ЛИТЕРАТУРА

1. Гультяев А. П. Визуальное моделирование в среде MATLAB: учеб. курс/ А. П. Гультяев.– СПб.: Питер, 2000.– 432 с.

2. Дьяконов В. П. MATLAB: учеб. курс/ В.П. Дьяконов. – СПб.: Питер, 2001.– 560 с.

3. Дьяконов В.П. Simulink 4. Специальный справочник / В.П. Дьяконов.– СПб.: Питер, 2002.– 528 с.

4. Кетков Ю.Л. MATLAB 6.x . Программирование численных методов / Ю Л Кетков, А. Ю Кетков, М.М. Шульц.– СПб.: БХВ-Петербург, 2004.–672 с.

5. Конев В.Ю. Основные функции пакета MATLAB: учеб.пособие/ В.Ю. Конев, Л.А. Мироновский.– 2-ое издание.– СПб.: ГААПСПб., 1994.–76 с.

6. Потемкин В. Г. Система MATLAB: справочное пособие/ В. Г. Потемкин.– М.: ДИАЛОГ-МИФИ, 1997.– 350 с.

7. Хакен Г. Синергетика: иерархии неустойчивостей в самоорганизующихся системах и устройствах. М.: Мир, 1985. 423 с.

8. Forsythe G. E. Computer Methods for Mathematical Computations./ Forsythe G. E., Malcolm M. A., Moler C. B. – Prentice-Hall, 1977.

9. SIMULINK. User’s Guide. Natick: The MathWorks, Inc., 1990