Обзор блоков раздела Sources

Практически любая модель в SIMULINK не обходится без блоков из трех разделов: Sources, Sinks и Math Operations.

Ознакомимся с наиболее часто используемыми блоками из этих библиотек. Для этого создадим новую модель (рис. 7.14).

Для создания блок-схемы сначала необходимо открыть раздел Sinks и перетащить в модель блок Scope, затем скопировать его 11 раз. После этого следует открыть раздел Sources, перетащить и разместить источники сигналов в модель, согласно рис. 7.14, после чего провести связи. Затем следует запустить модель нажатием на пиктограмму.

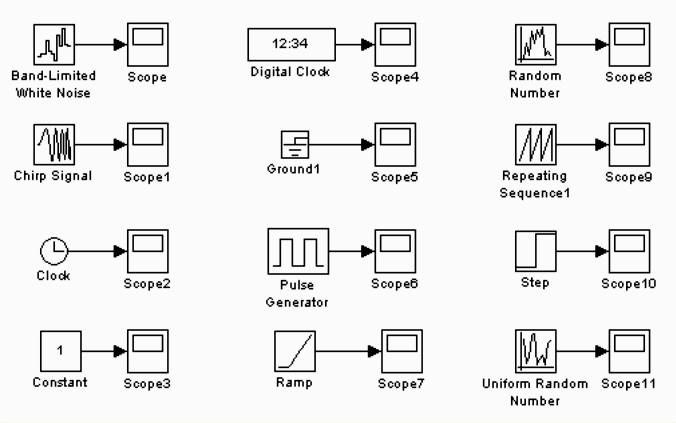
Рисунок 7.14 – Знакомство с блоками раздела Sources

Генерируемые блоками сигналы просматриваются путем двойного нажатия на соответствующем блоке Scope. После окончания просмотра следует сохранить модель под именем.

Рисунок 7.15 – Знакомство с блоками раздела Math Operations

Исследование блоков раздела Continuous

Практически все блоки, необходимые для создания линейных непрерывных систем, находятся в разделе Continuous библиотеки SIMULINK, исключение составляют блоки Sum, Product, Gain, которые находятся в библиотеке Math Operations. Для исследования их работы создадим блок-схему (рис. 7.16), изменим параметр в блоке Constant с 1 на 3, сохраним полученную модель под именем «pr31» и запустим. Результаты моделирования приведены в правой части рис. 7.16. Видно, что блок Derivative осуществляет операцию вычисления производной входного сигнала (выброс в момент перепада входного сигнала), блок Integrator -– интегрирование входного сигнала (линейно нарастающий сигнал), а блоки Transport Delay и Variable Transport Delay – задержку входного сигнала на постоянную и переменную величину времени.

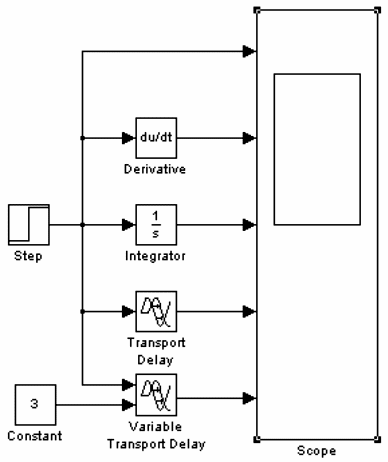
Рисунок 7.16 – Исследование блоков раздела Continuous

Модель простейшей системы автоматического регулирования

Рассмотрим пример работы автопилота. Система должна поддерживать заданную высоту полета самолета (1000 м) при воздействии факторов, приводящих к случайным колебаниям высоты в пределах 10 м. Для создания блок–схемы перетащим в новое окно редактора блоки Constant, Uniform Random Number, Transfer Fcn, Sum, Scope, Gain, Mux. Список параметров, которые необходимо изменить, приведены в табл. 7.1. Время моделирования установим равным 3600с, сохраним блок–схему под именем «pr32» и запустим на моделирование. Если все сделано правильно, результат будет аналогичным, приведенному на рис. 7.17.

Сигнал с большим размахом – траектория движения самолета без автопилота, сигнал с меньшим размахом – траектория движения в случае работы системы автоматического регулирования.

Таблица 7.1 – Список изменяемых параметров блоков

Блок	Параметр	Новое значение
Constant, Constant1, Constant2	Constant value	1000
Transfer Fcn, Transfer Fcn1	Denominator	[100 0]
Uniform Random Number и Uniform Random Number1	MinimumMaximum	–1010
Sum	List of signs	|+–
Gain	Gain	5

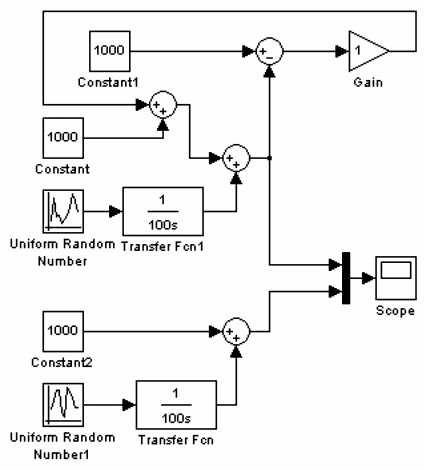
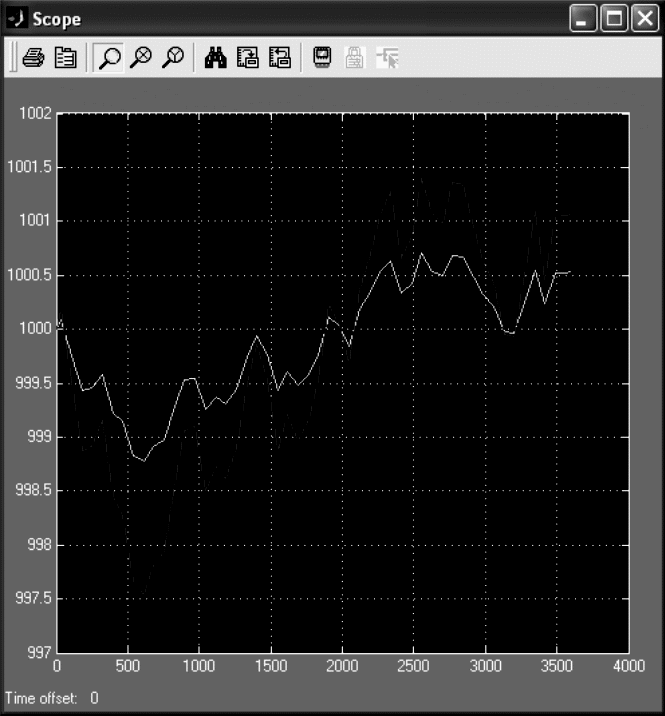
Рисунок 7.17 – Модель простейшей системы автоматического регулирования

 Рассмотрим пример построения модели с нелинейным элементом в цепи обратной связи и исследование устойчивости системы (рис. 7.18).

Рисунок 7.18 − построение модели с нелинейным элементом в цепи обратной связи

Для построения фазового портрета для данной модели используются узел дифференцирования (du/dt) и узел отображения информации по двум координатам (XY Graph). При этом получаем следующий фазовый портрет (рис. 7.19):

Рисунок 7.19 − фазовый портрет модели

Таким образом, из анализа графика можно сделать вывод, что эта система является устойчивой.

В разделе Simulink Extras находится дополнительная библиотека блоков Simulink.

П ример: моделирование в среде Simulink колебательной системы (рис. 7.20)

Рисунок 7.20 – Моделирование в среде Simulink колебательной системы

Блок алгебраического контура Algebraic Constraint выполняет поиск корней алгебраических уравнений.

Параметры: Initial guess – начальное значение выходного сигнала.

Блок находит такое значение выходного сигнала, при котором значение входного сигнала становится равным нулю.

На рис. 7.21 показан пример решения системы нелинейных уравнений вида:

Поскольку данная система уравнений имеет два решения, то начальные значения блоков Algebraic Constraint заданы в виде векторов. Для первого (верхнего) блока начальное значение задано вектором [1 -1], а для второго (нижнего) блока – вектором [-1 1].

Рисунок 7.21 – пример решения системы нелинейных уравнений

Subtract – Math Operations. В параметрах в окошке List of Signs надо поставить те операции, которые необходимы( - +).

Math Function - Math Operations. В параметрах в окошке Function надо выбрать square (чтобы был квадрат значения).

Algebraic Constant - Math Operations. В параметрах в окошке Initial guess задать начальное значение вектором [1 -1] или [-1 1].

Display – Sinks. выводит результат.