- •Функції однієї змінної. Границя, неперервність Основні означення та формули
- •Границя послідовності
- •Н. М. Послідовність
- •Властивості збіжних послідовностей
- •Монотонні послідовності
- •Підпослідовність
- •§ 7. Значення деяких границь
- •Границя функції
- •Нескінченно малі функції
- •Властивості функцій, що мають границю
- •Обчислення границь. Невизначеності
- •Виділення головної частини до першого порядку малості при
- •Виділення головної частини до другого порядку малості при
- •Неперервні функції.
- •Неперервність елементарних функцій
- •Класифікація точок розриву
- •Класифікація точок розриву
- •Основні теореми про неперервні функції
- •Теореми про неперервність монотонної, складної й оберненої функції
- •Теореми про обмеженість неперервної функції
- •Рівномірна неперервність
- •Зразки контрольних робіт.
- •Варіанти індивідуального завдання
Рівномірна неперервність
Означення.
Функція
називається рівномірно неперервною
на відрізку
,
якщо
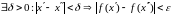
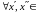 .
.
У цьому
випадку
залежить тільки від
і не залежить від вибору
 ,
згодиться
,
згодиться
 .
.
Побудуємо
заперечення рівномірної неперервності.
 ,
(або множині
)
такі, що хоча
,
(або множині
)
такі, що хоча
 .
.
Приклад
1.
на
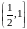 .
.
Шукаємо
.
.
.
Шукаємо
.

 .
.
Беремо

 знайшли
знайшли
 .
- рівномірно неперервна на
.
- рівномірно неперервна на
 .
.
Приклад
2.
на
 .
.
 .
Шукати
не будемо.
.
Шукати
не будемо.
Візьмемо
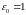 ,
,
 ,
,
 при цьому
при цьому
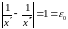 ,
,
А
відстань
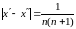 можна зробити менше для
можна зробити менше для
 .
.
Рівномірної
неперервності для
 на
немає.
на
немає.
Однак, чудово те, що в замкненому проміжку такого бути не може.
Теорема Кантора. Якщо функція неперервна на відрізку, то вона рівномірно неперервна на ньому.
Зразки контрольних робіт.
Контрольна робота №2
1.
Записати на мові
та намалювати ескіз графіка: а) 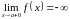 ;
б)
;
б)  .
.
2. Дослідити на неперервність та вказати характер точок розриву;
а)  ;
б)
;
б)  .
.
3.
Знайти границі: а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  ;
д)
;
д)  ;
е)
;
е) 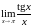 ;
ж)
;
ж)  ;
з)
;
з) 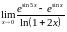 .
.
Варіанти індивідуального завдання
Индивидуальное задание № 2 «Предел последовательности и функции»
Задание № 1
1) Доказать, что для всех n
 Ν
выполнено
Ν
выполнено
 .
.
Найти все n Ν, для которых выполнено + ε, где ε равно: а) 1/6, б) 1/10, в) ½ (2k+1), k Ν.
2)
Доказать, что
выполнено
 .
.
1) Для каждого данного ε указать такое N, что выполнено
 <
ε
<
ε
для любого n ≥ Ν, и заполнить таблицу
ε |
1 |
0,2 |
10-2 |
10-4 |
N |
|
|
|
|
2)
Доказать, что

1) Для последовательности заполнить таблицу
ε |
10 |
0,5 |
0,03 |
3·10-4 |
7·10-10 |
N |
|
|
|
|
|
указав для каждого
данного ε
такое натуральное N,
что
< ε
для любого n
≥ Ν, если
 .
.
2)
Доказать, что
 .
.
Доказать, что последовательность {1/
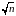 }
бесконечно малая. Для каждого данного
ε указать
такое натуральное N,
что 1/
< ε для
любого n ≥
Ν, и заполнить
таблицу:
}
бесконечно малая. Для каждого данного
ε указать
такое натуральное N,
что 1/
< ε для
любого n ≥
Ν, и заполнить
таблицу:
ε
10
1
0,1
0,01
N
Доказать, что последовательность
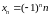 имеет бесконечный предел при
имеет бесконечный предел при
 (т. е. является бесконечно большой),
определив для всякого E>0
N
= N
(E)
такое, что
(т. е. является бесконечно большой),
определив для всякого E>0
N
= N
(E)
такое, что
 >Е
при n
> N,
и заполнить следующую таблицу:
>Е
при n
> N,
и заполнить следующую таблицу:
Е |
10 |
100 |
1000 |
10000 |
… |
N |
|
|
|
|
|
Задание № 2
Доказать, что - бесконечно малая последовательность, если:
 .
.Доказать, что - бесконечно малая последовательность, если:

Доказать, что последовательность расходится, если:
 .
.Доказать, что последовательность расходится, если:

Доказать, что последовательность расходится, если:

Задание № 3
1. Доказать, что
 .
.
2. Доказать, что
 где p
≥ 1.
где p
≥ 1.
3. Доказать, что
 .
.
4. Доказать, что
 .
.
5. Доказать, что
 ,
где а >1, p
≥ 1.
,
где а >1, p
≥ 1.
Задание № 4
Для последовательности
 найти множество частичных пределов,
найти множество частичных пределов,
 ,
,

Для последовательности
 найти
множество частичных пределов,
,
.
найти
множество частичных пределов,
,
.
Для последовательности
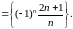 найти множество частичных пределов
,
.
найти множество частичных пределов
,
.Для последовательности
 найти множество частичных пределов
,
.
найти множество частичных пределов
,
.Найти множество частичных пределов последовательности:

Задание № 5
Для последовательности
 найти множество частичных пределов
,
,
найти множество частичных пределов
,
,
 ,
,
 .
.Для последовательности
 найти множество частичных пределов
,
,
,
.
найти множество частичных пределов
,
,
,
.Для последовательности
 найти множество частичных пределов
,
,
,
найти множество частичных пределов
,
,
,
Для последовательности
 найти
,
,
а также
,
найти
,
,
а также
,
Для последовательности
 найти
,
,
а также
,
найти
,
,
а также
,
Задание № 6
Найти

Найти
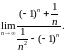
Найти

Найти

Найти

Задание № 7
1. Найти

2. Найти

3. Найти

4. Найти

5. Найти

Задание № 8
Найти

Найти
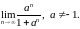
Найти

Найти

Найти

Задание № 9
Найти

Найти

Найти
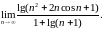
Найти

Найти
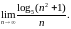
Задание № 10
Найти

Найти

Найти

Найти

Найти

Задание № 11
Для функции
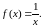 заполнить
таблицу
заполнить
таблицу
|
0,9 |
0,5 |
0,1 |
0,01 |
-0,9 |
-0,5 |
-0,1 |
-0,01 |
|
|
|
|
|
|
|
|
|
указав для данного
приращения
 соответствующее приращение функции
соответствующее приращение функции
 ;
построить график функции f
и указать на нём точки, соответствующие
;
построить график функции f
и указать на нём точки, соответствующие
 и
и
 :
:
Для функции
 заполнить
таблицу
заполнить
таблицу
|
0,9 |
0,5 |
0,1 |
0,01 |
-0,9 |
-0,5 |
-0,1 |
-0,01 |
|
|
|
|
|
|
|
|
|
указав для данного приращения соответствующее приращение функции ; построить график функции f и указать на нём точки, соответствующие и :
Для функции
 заполнить таблицу
заполнить таблицу
|
0,9 |
0,5 |
0,1 |
0,01 |
-0,9 |
-0,5 |
-0,1 |
-0,01 |
|
|
|
|
|
|
|
|
|
указав для данного приращения соответствующее приращение функции ; построить график функции f и указать на нём точки, соответствующие и :
Для функции
 заполнить
таблицу
заполнить
таблицу
|
0,9 |
0,5 |
0,1 |
0,01 |
-0,9 |
-0,5 |
-0,1 |
-0,01 |
|
|
|
|
|
|
|
|
|
указав для данного приращения соответствующее приращение функции ; построить график функции f и указать на нём точки, соответствующие и :
5. Для функции
заполнить таблицу, указав для каждого
значения
наибольшее значение
так, чтобы для любого
 из неравенства
из неравенства
 следовало
неравенство
следовало
неравенство
 :
:
|
0 |
1/16 |
1/4 |
25/81 |
1 |
4 |
|
|
|
|
|
|
|
Задание № 12
Найти: а)
 ;
б)
;
б)
 :
:  ,
.
,
.Найти: а) ; б) :
 ,
,
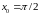 .
.Найти: а) ; б) :
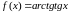 ,
.
,
.Найти: а) ; б) :
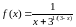 ,
,
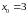 .
.Найти: а)
 ;
б)
;
б)
 :
: 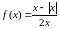 .
.
Задание № 13
Найти
 и
и
 ,
если:
,
если:
 .
.Найти и , если:
 .
.Найти и , если:
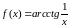 .
.Найти и , если:
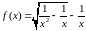 .
.Найти и , если:
 .
.
Задание № 14
Пользуясь определением, доказать:
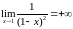 .
.Пользуясь определением, доказать:
 .
.Пользуясь определением, доказать:
 .
.Пользуясь определением, доказать:
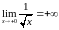 .
.Пользуясь определением, доказать:
 .
.
Задание № 15
Найти предел функции:
 .
.Найти предел функции:
 .
.Найти предел функции:
 .
.Найти предел функции:
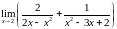 .
.Найти предел функции:
 .
.
Задание № 16
1. Найти предел
функции:
 .
.
2. Найти предел
функции:
 .
.
3. Найти предел
функции:
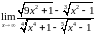 .
.
4. Найти предел
функции:
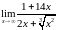 .
.
5. Найти предел
функции:
 .
.
Задание № 17
1. Найти предел
функции:
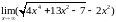 .
.
2. Найти предел
функции:
 .
.
3. Найти предел
функции:

4. Найти предел
функции:
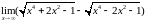 .
.
5. Найти предел
функции:
 .
.
Задание № 18
1. Найти предел
функции: .
.
2. Найти предел
функции: .
.
3. Найти предел
функции: .
.
4. Найти предел
функции: .
.
5. Найти предел
функции: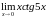 .
.
Задание № 19
1. Найти предел
функции: .
.
2. Найти предел
функции: .
.
3. Найти предел
функции: .
.
4. Найти предел
функции: .
.
5. Найти предел
функции: .
.
Задание № 20
1. Найти предел
функции: .
.
2. Найти предел
функции: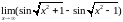 .
.
3. Найти предел
функции: .
.
4. Найти предел
функции: .
.
5. Найти предел
функции: .
.
Задание № 21
1. Найти предел
функции: .
.
2. Найти предел
функции: .
.
3. Найти предел
функции: .
.
4. Найти предел
функции: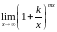 .
.
5. Найти предел
функции: .
.
Задание № 22
1. Найти предел
функции:
 .
.
2. Найти предел
функции:
 .
.
3. Найти предел
функции:
 .
.
4. Найти предел
функции:
 .
.
5. Найти предел
функции:
 .
.
Задание № 23
1. Найти: а)
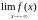 ;
б)
;
б)
 :
:  .
.
Найти: а) ; б) :
 .
.
3. Найти предел
функции:  .
.
4. Найти: а)
;
б)
: 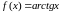 .
.
5. Найти: а)
 ;
б)
;
б)
 :
:  .
.
Задание № 24
1. Найти предел
функции: ,
a
>0.
,
a
>0.
2. Найти предел
функции: .
.
3. Найти предел
функции: .
.
4. Найти предел
функции: .
.
5. Найти предел
функции: .
.
Задание № 25
1. Найти предел
функции: .
.
2. Найти предел
функции: .
.
3. Найти предел
функции: .
.
4. Найти предел
функции: .
.
5. Найти предел
функции: .
.
Задание № 26
1. Найти предел
функции:
 .
.
2. Найти предел
функции:
 .
.
3. Найти предел
функции:
 .
.
4. Найти предел
функции: .
.
5. Найти предел
функции:
 .
.
Задание № 27
Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода:
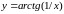 .
.Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода:
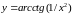 .
.Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода:
 .
.Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода:
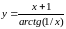 .
.Найдите точки разрыва функции, установите их род, найдите скачки в точках разрыва 1-го рода:
 .
.
Задание № 28
1. Найдите точки
разрыва функции, установите их род,
доопределите функцию по непрерывности
в точках устранимого разрыва:  .
.
2. Найдите точки
разрыва функции, установите их род,
доопределите функцию по непрерывности
в точках устранимого разрыва:  .
.
3. Найдите точки
разрыва функции, установите их род,
доопределите функцию по непрерывности
в точках устранимого разрыва:  .
.
4. Найдите точки
разрыва функции, установите их род,
доопределите функцию по непрерывности
в точках устранимого разрыва:  .
.
5. Найдите точки
разрыва функции, установите их род,
доопределите функцию по непрерывности
в точках устранимого разрыва:  .
.
Задание № 29
При каком значении а функция
 будет непрерывна.
будет непрерывна.При каком значении а функция
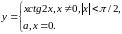 будет непрерывна.
будет непрерывна.При каком значении а функция
 будет непрерывна.
будет непрерывна.При каком значении а функция
 будет непрерывна.
будет непрерывна.При каком значении а функция
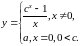 будет непрерывна.
будет непрерывна.
Задание № 30
1. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:

2. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:

3. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:

4. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:

5. Указать множество точек, в которых непрерывна функция, найти её точки разрыва, установить их род, нарисовать график функции:

Задание № 31
1. Для ε
> 0 найти
 (какое-нибудь!), удовлетворяющее условиям
равномерной непрерывности для функции
(какое-нибудь!), удовлетворяющее условиям
равномерной непрерывности для функции
 на данном промежутке, если:
на данном промежутке, если:


2. Доказать, что функция f равномерно непрерывна на множестве Х, если:

3. Для ε > 0 найти (какое-нибудь!), удовлетворяющее условиям равномерной непрерывности для функции на данном промежутке, если:


4. Доказать, что функция f равномерно непрерывна на множестве Х, если:

5. Для ε > 0 найти (какое-нибудь!), удовлетворяющее условиям равномерной непрерывности для функции на данном промежутке, если:


Задание № 33
1. Исследовать на
равномерную непрерывность в заданной
области функцию
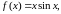

2. Исследовать на
равномерную непрерывность в заданной
области функцию


3. Исследовать на
равномерную непрерывность в заданной
области функцию

4. Исследовать на
равномерную непрерывность в заданной
области функцию


5. Исследовать на
равномерную непрерывность в заданной
области функцию