
- •Функції однієї змінної. Границя, неперервність Основні означення та формули
- •Границя послідовності
- •Н. М. Послідовність
- •Властивості збіжних послідовностей
- •Монотонні послідовності
- •Підпослідовність
- •§ 7. Значення деяких границь
- •Границя функції
- •Нескінченно малі функції
- •Властивості функцій, що мають границю
- •Обчислення границь. Невизначеності
- •Виділення головної частини до першого порядку малості при
- •Виділення головної частини до другого порядку малості при
- •Неперервні функції.
- •Неперервність елементарних функцій
- •Класифікація точок розриву
- •Класифікація точок розриву
- •Основні теореми про неперервні функції
- •Теореми про неперервність монотонної, складної й оберненої функції
- •Теореми про обмеженість неперервної функції
- •Рівномірна неперервність
- •Зразки контрольних робіт.
- •Варіанти індивідуального завдання
§ 7. Значення деяких границь
№58.
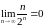 №59.
№59.
 №60
№60
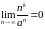 (
(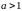 )
)
№61 №62.
№62.
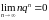 ,
,
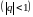 №63.
№63.
 (
(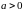 )
)
№64
 (
) № 65.
(
) № 65.
 № 66.
№ 66.
 .
.
Границя функції
Означення.
Інтервал
вигляду
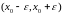 або
або
 називається
- околом точки
називається
- околом точки
 ,
та позначається
,
та позначається
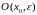 ,
,
 або
або
 .
.
Проколеним
околом точки
називається окіл точки
,
із якого викинута сама точка. Позначається
 .
.
Околом
" "
називається будь-який напівнескінченний
проміжок (промінь) вигляду
"
називається будь-який напівнескінченний
проміжок (промінь) вигляду
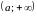 .
.
Околом
" "
називається будь-який промінь вигляду
"
називається будь-який промінь вигляду
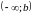 .
.
Околом
" "
називається об'єднання двох околів
"
називається об'єднання двох околів
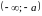 та
.
та
.
Означення.
Точка
називається граничною точкою множини
 ,
якщо в будь-якому околі точки
знайдеться точка
,
якщо в будь-якому околі точки
знайдеться точка
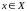 така, що
така, що
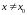 .
.
З начення
границі функції пояснимо на графіку.
начення
границі функції пояснимо на графіку.
При наближенні до значення функції прямують до .

 при
при
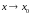 .
.
Означення можна дати як мовою послідовності, так і мовою околів.
Нехай
точка
є граничною точкою
 .
Нехай функція
.
Нехай функція
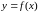 визначена в деякому околі точці
,
окрім, може бути, самої цієї точки, тобто
в
.
визначена в деякому околі точці
,
окрім, може бути, самої цієї точки, тобто
в
.
Def
(за
Гейне).
Число
називається границею функції
 при
,
якщо
при
,
якщо
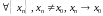 виконане
виконане
 .
.
Def (за
Коши). Число
називається границею функції
при
,
якщо для будь-якого як завгодно малого,
наперед заданого
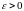 існує таке
існує таке
 ,
що для всіх
,
що для всіх
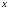 таких, що
таких, що
 виконується нерівність
виконується нерівність
 .
Або символами
.
Або символами


 .
.
(lim - скорочене слово limit ‑ границя).
Теорема (про рівносильність двох означень границі). Якщо функція має границю в точці за означенням Коши, то вона має границю й за означенням Гейне і навпаки.
Границя, яку ми розглядали за допомогою двобічного околу, називається двобічною.
Можливі, однак, однобічні границі.
При
цьому,
 - ліва границя;
- ліва границя;
 - права границя.
- права границя.
У першому
випадку
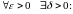
 ;
;
У другому
 .
.
Завдання
для самостійного розв’язання. Для
того щоб
мала в точці
 двобічну границю, необхідно й достатньо,
щоб вона мала в цій точці праву й ліву
границі й вони були рівні.
двобічну границю, необхідно й достатньо,
щоб вона мала в цій точці праву й ліву
границі й вони були рівні.
Нескінченно малі функції
Означення.
Функція
 називається
нескінченно малою функцією (н.м.), або
просто нескінченно малою при
,
якщо
називається
нескінченно малою функцією (н.м.), або
просто нескінченно малою при
,
якщо
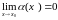 .
.
Н.м. функції мають важливу роль (як і н.м. послідовності). Це пов'язане з тим, що загальне поняття границі може бути зведеним до поняття н.м.
Властивість
1. Границя
функції
в точці
й дорівнює числу
тоді й тільки тоді, коли функція
може бути представленою у вигляді
 ,
де
- н.м. при
.
,
де
- н.м. при
.
Властивість 2. Сума двох н.м. функцій при є н.м.
,
 - н.м.
- н.м.
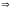
 - н.м.
- н.м.
Властивість 3. Добуток двох н.м. функцій при є н.м. функція.
,
- н.м.
 - н.м.
- н.м.
Зауваження. Властивості 2 і 3 справедливі для скінченої кількості доданків (множників).
Властивість 4. Добуток н.м. функції на обмежену при є функція н.м.
Означення.
Функція
називається н.в. при
,
якщо
 ,
тобто якщо
,
тобто якщо
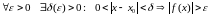 .
.
Властивість
5. Функція
(
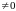 ,
,
 )
є н.м. при
тоді й тільки тоді, коли
)
є н.м. при
тоді й тільки тоді, коли
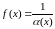 є н.в.
є н.в.
За аналогією зі скінченими однобічними границями, впровадимо означення й однобічних нескінчених границь.

 .
.
Нескінченності
додатна та від'ємна - це не числа, їх
можна додати до множини дійсних чисел
 як нові елементи
як нові елементи
 .
Після цього числова пряма перетворюється
в так називану розширену пряму.
.
Після цього числова пряма перетворюється
в так називану розширену пряму.
