Функції однієї змінної. Границя, неперервність Основні означення та формули

Означення. Якщо існує закон, за яким кожному натуральному числу ставиться у відповідність певне відповідне дійсне число, то кажуть, що задано послідовність дійсних чисел.

Означення. Функція, що визначена на 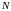називається послідовністю

, , .

Ч исло, що відповідає 1 будемо називати першим членом послідовності ... Число, що відповідає числу , будемо називати - м членом послідовності.

Геометричне зображення послідовності. Графіком послідовності буде набір точок.

Способи завдання послідовності

1. Явне завдання (аналітичне). Задається формулою: ; , .

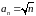2. Рекурентне завдання (теж формулою, але неявно). Воно полягає в тому, що дається декілька перших членів і вказується спосіб обчислення - го члена за допомогою попередніх:

;

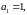
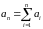
(арифметична прогресія)

Означення. Множина - зліченна, якщо між його членами й натуральними числами існує взаємно однозначна відповідність. Тоді послідовність – набір зліченної кількості дійсних чисел, які пронумеровані й поставлені в чергу .

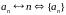Границя послідовності

Означення. Послідовність називається обмеженою зверху, якщо множина її значень обмежена зверху, тобто таке, що .

Послідовність називається обмеженою знизу, якщо множина її значень обмежена знизу, тобто таке, що .

Послідовність називається обмеженою, якщо такі, що 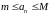або таке, що .

Якщо зі зростанням номера послідовність прямує до якого-небудь числа, то ми приходимо до поняття границі.

Означення. Число називається границею числової послідовності , якщо ( ).

Означення. Якщо послідовність має границю, то кажуть, що вона збігається. Послідовність, яка не є збіжною, називається розбіжною.

Це означення скінченої границі.

Якщо ж із зростанням номера значення послідовності необмежено зростають, то ми маємо нескінченно велику (н.в.) послідовність, тобто послідовність має нескінченну границю.

Означення. Послідовність називається н.в. якщо 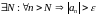. Позначення .

Зауваження. Потрібно пам'ятати правило формування зворотного твердження: потрібно поміняти місцями значки і , а знак нерівності на протилежний. Наприклад, послідовність не є н.в., якщо,

Твердження. Будь яка н.в. послідовність не обмежена. Зворотне твердження невірно. Приклад: .

Завдання для самостійного розв'язання. Записати мовою й навести приклад якщо 1) ; 2)

Схема розв'язання прикладів на доведення

Для розв'язання необхідно взяти параметр , зафіксувати його, і шукати таке, щоб виконувалося .

Причому бажано дістати як можна простіше (краще за все ) збільшуючи його, але щоб 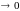при . І потім розв'язуємо .

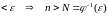Н. М. Послідовність

Означення. Послідовність називається нескінченно малою (н.м.), якщо , або .

Звичайно, н.м. послідовності позначаються , .

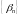Відзначимо кілька властивостей н.м. послідовностей.

Властивість 1. Якщо послідовність н.м., то вона обмежена.

Властивість 2. Сума двох н.м. послідовностей є н.м., різниця двох н.м. є н.м.

Наслідок. Сума й різниця будь-якої скінченої кількості н.м. є н.м.

Завдання для самостійного розв'язання. Навести приклад, коли сума нескінченної кількості н.м. не є н.м.

Властивість 3. Добуток н.м. на обмежену послідовність є н.м.

Наслідок. Добуток скінченого числа н.м. є н.м.

Зауваження. Добуток нескінченного числа н.м. не обов'язково н.м.

Приклад. - н.в.

Завдання для самостійного розв'язання

1. Відомо, що . Чи випливає звідси, що

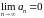А) та .

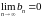Б) Хоча б одна з послідовностей ‑ н.м.

2. Нехай , де

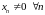
А) Чи існує ?

Б) Довести, що якщо ця границя існує та дорівнює , то .

В) Чи може послідовність 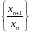бути необмеженою?

Властивість 4. Якщо послідовність ( ) н.м., то н.в.

Властивість 5. Для того, щоб число було границею послідовності необхідно й достатньо щоб різниця була н.м.

Наслідок. Послідовність має скінчену границю тоді й тільки тоді, коли її можна записати у вигляді , де - н.м.