2. Ќоординаталыќ әдістер
Евклид кеңістігінде кез келген нүктенін, орны координаталары деп аталатын өзара тәуелсіз үш скаляр шамамен бір мәнді анықталатыны белгілі. Олар сызыќтыќ немесе бұрыштық шамалар болып келулері мүмкін. Нүкте қозғалысы кезінде оның координаталары уақыт өтуі-мен байланысты өзгеріп отырады, яғни олар уаќыттың үздіксіз функциялары болып табылады. Бұл функциялар нүктенің координатальтќ түрдегі қозғалыс теңдеулері деп аталатын үш скалярлыќ теңдеуді береді.
Таңдап алынған координаталар системасында нүкте қозғалысының параметрлік (параметр ретінде кебіне уақыт ќатысады) теңдеулері белгілі болса, қоғалыс координаталыќ әдіспен берілген деп есептейміз.
Нүкте қозғалысының скалярлыќ теңдеулерінің түрі қозғалыстың қандай координаталар системасында ќарастырылуына байланысты. Координаталар системалары түзу сызыќты және қисыќ сызыќты болып екі топқа бөлінеді. Бірінші топтан біз тек тік бұрышты декарттыќ координаталар системасын ѓана пайдаланамыз. Кейбір есептерді шешуде ортогональдық қисыќ сызыќты координаталар системалары пайдаланған да тиімді.
2.1. Түзу сызыќты декарттық координаталар әдісі.
Нүктенің
кеңістіктегі қозғалысын зерттеу үшін
тік бұрышты декарттыќ координаталар
системасын таңдап аламыз (6-сурет). Әдетге
оң координаталар системасы ќарастырылады,
яғни координаталар осьтері оњ бүрѓы
(винт) ережесі бойынша;
осініњ
оң бағытынан қараѓанда
осініњ оң бағытын
осінің оң бағытына қарай ең қысқа жолмен
бұру сағат тілінің жүрісіне қарсы
бағытта орындалатындай етіп таңдап
алынады.
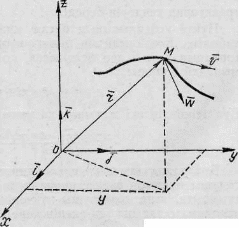
6-сурет.
Бұл системада нүктесінің қозғалысы оның параметрлік теңдеулерімен
(11)
яғни
(1) радиус-векторыныњ координаталар
осьтеріндегі проекциялары арқылы
берілсін. Нүкте координаталары оның
системаның
бас нүктесіне қарағандағы радиус-векторының
сәйкес
координаталар осьтеріне проекциялары
болѓандыќтан (11) теңдеулері нүкте
қозғалысының векторлыќ теңдеуінің (1)
координаталар осьтеріне проекциялары
болады.
Бір мәнді, үздіксіз және кемінде екі рет дифференциалданатын (11) функцияларын нүктесініњ сәйкес осьтер бойындаѓы қозғалыс заңдары деуге болады. Бұл мағынада қисыќ сызыќты ќозѓалыс координаталар осьтерінің бойымен алғандағы үш түзу сызыќты қозғалысқа жіктеледі. Ќеңістікте (11) теңдеулері белгілі бір қисыќтың, яғни нүкте траекториясының параметрлік теңдеулері болады. Бұл теңдеулерден ќозғалушы нүктенің жалѓас уаќыт кезеңдеріндегі координаталарын тауып, оның траекториясын ќұруѓа болады.
Траекторияның теңдеуін координаталыќ түрде алу үшін (11) тең-деулерінен уақытты жою керек. Сонда қиылысу сызығы қозғалушы нүктенің траекториясын беретін екі цилиндрлік беттің теңдеуі табылады.