1 Геометрические характеристики плоских сечений

Этот раздел посвящен ознакомлению со свойствами и методами вычисления специальных геометрических характеристик плоских сечений элементов конструкций, используемых при расчете на прочность при изгибе, при изгибе с растяжением (сжатием), при кручении и в ряде других случаев.

1.1 Теоретическая часть

Статическими моментами площади поперечного сечения относительно осей X и Y называются определенные интегралы вида

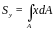, , (1.1)

где A - площадь поперечного сечения;

х, у - координаты элементарной площади dA;

S_x и S_y - соответственно статический момент относительно оси X и

статический момент относительно оси Y.

Рисунок 1.1 Рисунок 1.2

Статические моменты могут иметь знак «+», знак «-» и равны нулю. Размерность – м³, см³, мм³.

Если известно положение центра тяжести (цт) сечения (рисунок 1.2), то статический момент сечения можно считать по формулам

, , (1.2)

где X_С, Y_С – координаты центра тяжести сечения.

Из зависимостей (1.2) можно найти положение центра тяжести (цт)

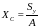, . (1.3)

Если сложное сечение состоит из простых фигур (допустим из 3-х фигур), то центр тяжести этого сечения можно определить по следующим формулам

,

(1.4)

,

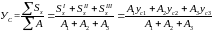где А₁, А₂, А₃ - площади отдельных фигур сечения;

х_c1, х_c2, х_c3, у_c1, у_c2, у_c3 – координаты цт отдельных фигур относительно

любых вспомогательных осей X и Y.

Осевыми моментами инерции сечения относительно осей X и Y (рисунок 1.1) называются определенные интегралы вида

, . (1.5)

Осевые моменты всегда положительны и имеют размерность м⁴, см⁴, мм⁴.

Центробежным моментом инерции сечения относительно 2-х взаимно перпендикулярных осей X и Y называется определенный интеграл вида

. (1.6)

Он может иметь знак «+» или «–» и равным нулю.

Имеет размерность м⁴, см⁴, мм⁴.

Полярным моментом инерции сечения относительно полюса «0» называется определенный интеграл вида

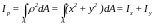, (1.7)

где ρ – расстояние от элементарной площади до полюса «0».

Полярный момент инерции всегда положителен и равен сумме 2-х осевых моментов инерции, имеет размерность - м⁴, см⁴, мм⁴.

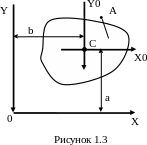
Вычисление момента инерции при параллельном переносе осей (рисунок 1.3)

Главные центральные оси – центральные оси, относительно которых центробежный момент инерции сечения (I_хy, D_xy) равен нулю.

Главные центральные моменты – осевые моменты инерции сечения относительно главных центральных осей.

, , (1.8) , где X0, Y0 – центральные оси сечения; X, Y - любые параллельные оси сечения; а, b – соответственно расстояние между осями X, X0 и Y, Y0.

Положение главных центральных осей определяется уравнением

, (1.9)

где , , – соответственно осевые моменты инерции и центробежный

момент инерции относительно центральных осей сечения X₀, Y₀;

α₀ – угол между осью X₀ и главной центральной осью.

Если угол «α₀» положительный, то центральные оси X₀, Y₀ надо вращать против часовой стрелки.

Главные моменты инерции вычисляются по формуле

. (1.10)

Главные моменты инерции обладают признаком экстремальности: один из 2-х главных моментов имеет максимальное значение, а другой – минимальное значение из всех возможных значений моментов инерции относительно любых центральных осей. Обычно в задании главные центральные оси обозначают «U» и «V» соответственно главные моменты инерции обозначают через I_U и I_V.

Главные радиусы инерции вычисляются по формулам

, . (1.11)

Выводы

1 Относительно центральных осей X₀ и Y₀ статистические моменты равны нулю (S_х0 = 0, S_у0 = 0).

2 Центр тяжести сечения всегда находится на оси симметрии.

3 Если сечение имеет две оси симметрии, то центр тяжести (цт) находится на пересечении этих осей.

4 Главные центральные оси – оси, относительно которых статистические моменты и центробежные моменты равны нулю.

5 Главные моменты инерции – осевые моменты относительно главных центральных осей.

6 Главные моменты инерции обладают признаком экстремальности.

7 Если сечение имеет одну ось симметрии, то главными центральными осями будут эта ось симметрии и ей перпендикулярная центральная ось.

8 Если сечение имеет две оси симметрии, то эти оси являются главными центральными осями.

9 Значение осевых моментов инерции всегда положительны и имеют размерность – мм⁴, см⁴, м⁴.

10 Центробежный момент инерции может иметь знаки «+» и «-» и может быть равным нулю, размерность - мм⁴, см⁴, м⁴.

11 При повороте осей или всего сечения на 90⁰, знак центробежного момента изменяется на обратный.