СМОД – Статистические методы обработки данных / Лаба 1 - 8 / smodlabs / по смоду / шпоры_2006г / 41

41. Стационарные случайные последовательности, их характеристики(математическое ожидание, ковариационная функция, спектральная плотность).

Пусть задано некоторое вероятностное пространство {}.

Определение: случайным процессом называется действительная функция , измеримая при каждом t из . Т.о. случайный процесс определяется как функция двух аргументов - элементарный исход (случай); - время из некоторого промежутка времени .

Если зафиксировать аргумент t=t1, то получим функцию аргумента : , которая называется сечением случайного процесса в момент времени t1 и является случайной величиной.

Если зафиксировать элементарный исход (случай) w=w1, получим функцию времени которая называется траекторией (реализацией, выборочной функцией сложного процесса).

Реализация сложного процесса – x(t). Если -некоторый отрезок действий прямой(<=R1), то процесс называется процессом с непрерывным временем. Если -дискретное(конечное или счётное), то СП называется процессом с дискретным временем (случайные последовательности). Она может быть получена из процесса с непрерывным временем выборкой его значений в дискретные моменты времени.

Т.к.обычно (множество элементарных исходов) нам недоступно, то СП обозначается в виде функции одной переменной . Cлучайная последовательность обозначается i=0,1,2…(может быть меньше 0 (прошлое))-периодискретизация по времени.

Законы распределения СП

Конечномерной (n-мерной) функцией распределения СП называется совместная функция распределения её сечений в n произвольных моментах времени

Эта функция 2n –аргументов.

Одномерная

Конечномерной (n-мерной) плотностью вероятности СП называется смешанная производная n-го порядка по x1, …xn от n-мерной функции распределения:

Числовые характеристики СП называются моментами функции. Важнейшие: мат.ожидание, дисперсия, ковариационная функция. Мат.ожидание СП -функция , определяемая выражением: Это функция, вокруг которой группируются все возможные реализации СП. Мат.ожидание определяется одномерным законом распределения СП, в частности одномерной плотности вероятности.

Дисперсия СП – функция

Характеризует разброс реализаций СП относительно мат.ожидания для любого момента времени t. Также определяется одномерная плотность вероятности.

Ковариационная функция СП –это коэффициент ковариации между сечением СП в два разных момента времени.

Если СП имеет конечномерные плотности вероятностей, то она рассчитывается по формуле , где - двум. пл-ть вер-ти.

Определяется двумерным распределением и является функцией двух аргументов . Она характеризует силу линейной стохастической связи между двумя сечениями СП.

СП делится на стационарное и нестационарное ; в узком (строгом) смысле если его конечномерное распределение не зависит от сдвига по оси времени : для любого промежутка времени выполняется равенство:

СП называется стационарным в широком смысле, если его мат.ожидание не зависит от времени, т.е. ,а ковариационная функция зависит лишь от одного аргумента

Из стационарности в узком смысле всегда следует стационарность в широком смысле, обратное неверно; верно для гауссовских процессов.

Для стационарных процессов вводится понятие спектральной плотности: спектральная плотность и ковариационная функция – это пара преобразований Фурье , т.е.

,

Спектральная плотность представляет собой среднюю мощность процесса на частной составляющей с угловой частотой w

Дисперсия стац.процесса

, ,

Рассмотрим случайную последовательность ,которая получается выборкой значений случайного процесса в дискретные, равностоящие на T моменты времени.

Ковариационная функция этой последоваетльности –последовательность коэффициентов ковариации R(0T), R(T), R(2T), где

Имеет место св-во:

Для случайной последовательности также вводится понятие спектральной плотности : Спектральная плотность сл. последовательностиряд Фурье , коэффициентами которого являются значения ковариационной функции:

- ряд Фурье в комплексной форме

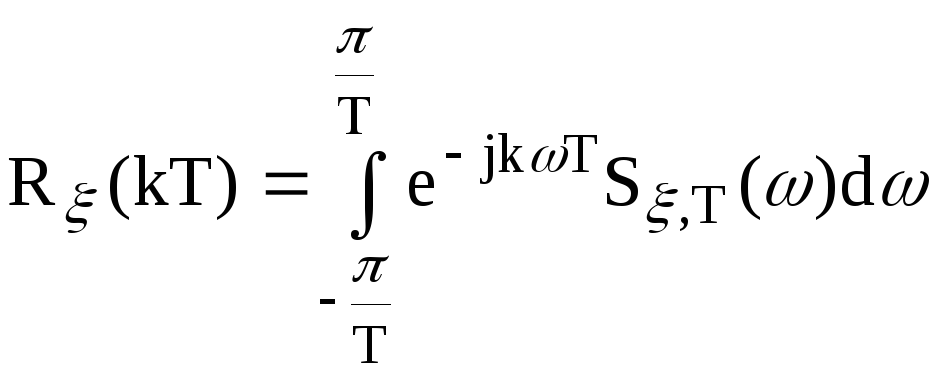
Функция, имеющая представление в виде ряда Фурье, является периодической с периодом . Поэтому спектральную плотность достаточно рассматривать на промежутке ()

Если воспользоваться формулой Эйлера , то ряд Фурье для спектральной плотности:

Если учесть нечётность sin и чётность R(KT), то мнимая часть=0.

- спектральная плотность – cos преобразования Фурье от ковариационной ф-ции и является действит. ф-цией.

Если учесть чётность cos и , то окажется, что есть одинаковые слагаемые:

При w=0 получим: .