СМОД – Статистические методы обработки данных / Лаба 1 - 8 / smodlabs / по смоду / шпоры_2006г / 40

40. Проверка гипотезы дисперсионного анализа.

Рассмотри выражение для . Преобразуем выражение:

Можно показать, что второе слагаемое равно 0, обозначим его z.

- не зависит от j, вынесем за сумму

Найдем:

Тогда:

(*), где

Умножим обе части равенства (*) на, получим:

,

где;;.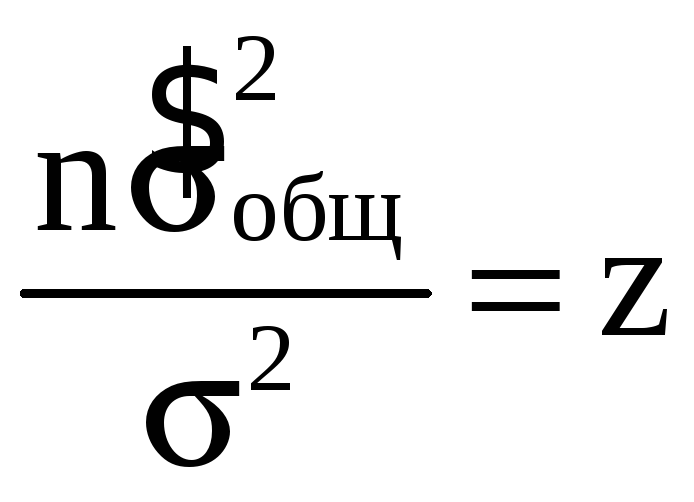

Получаем

Знаем, что величина, , если и независимы, то

По анологии с этим св-сом можно утверждать, что, т.е . Доказанно, что независемы.

В таком случаи известно, что величина (это f статистика для проверки гипотезы)

Критерий значимости для проверки гипотезы имеет вид

Если в выражении f подставить статистики, получим

Кроме того, в дисперсном анализе исп-сь не оценки дисперсии, а суммы квадратов:

,

статистика f записывается в виде: