1. Метод Гаусса вычисления определителя.

, т.е. определитель равен произведению ведущих элементов для соответствующей схемы Гаусса.

2. Свойство определителей.

1. При транспонировании матрицы её определитель не меняется.

2. Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.

3. Пусть 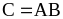где квадратные матрицы. Тогда .

4. Определитель с двумя одинаковыми строками или с двумя одинаковыми столбцами равен 0.

5. Определитель с двумя пропорциональными строками или столбцами равен 0.

6. Определитель треугольной матрицы равен произведению диагональных элементов.

7. Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число.

8. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором - вторые слагаемые.

3 Метод итераций. Достаточное условие сходимости метода итераций

Одним из наиболее эффективных способов численного решения уравнений является метод итерации. Сущность этого метода заключается в следующем. Пусть дано уравнение

.

Заменим его равносильным уравнением

. (1)

Выберем начальное приближение корня и подставим его в правую часть уравнения (1). Тогда получим некоторое число

. (2)

Подставляя теперь в правую часть (2) вместо число получим число . Повторяя этот процесс, будем иметь последовательность чисел

( ). (3)

Если эта последовательность сходящаяся, то есть существует предел , то переходя к пределу в равенстве (3) и предполагая функцию непрерывной найдем

или

.

Таким образом, предел является корнем уравнения (1) и может быть вычислен по формуле (3) с любой степенью точности.

Рис. 1а Рис. 1б

Р ис. 2. - расходящийся процесс

На рис.1а, 1б в окрестности корня и процесс итерации сходится. Однако, если рассмотреть случай , то процесс итерации может быть расходящимся (см. рис.2).

Сформулируем достаточные условия сходимости метода итерации.

Теорема. Пусть функция определена и дифференцируема на отрезке , причем все ее значения и пусть при . Тогда процесс итерации сходится независимо от начального значения и предельное значение является единственным корнем уравнения на отрезке .

4. Итерационные методы решения слау. Метод простой итерации. Достаточные условия сходимости.

Метод простой итерации. Достаточные условия сходимости.

Возьмём уравнение , преобразуем его к виду, удобному для итерации . Это преобразование можно выполнить различными способами. Функция называется итерационной функцией. Расчетная формула метода простой итерации имеет вид: .

 

Теорема о сходимости метода простой итерации. Пусть в некоторой - окрестности корня функция дифференцируема и удовлетворяет неравенству , где - постоянная . Тогда независимо от выбора начального приближения из указанной - окрестности итерационная последовательность не выходит из этой окрестности, метод сходится

со скоростью геометрической последовательности и справедлива оценка погрешности: , .

 

Критерий окончания итерационного процесса. При заданной точности >0 вычисления следует вести до тех пор пока не окажется выполненным неравенство . Если величина , то можно использовать более простой критерий окончания итераций: .

Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду . Предположим дополнительно, что производная знакопостоянна и на отрезке [a,b]. Тогда при выборе итерационного параметра метод сходится и значение

.