2. Пример выполнения задания №2

Конкретные условия примера выполнения домашнего задания будут здесь взяты из табл.2.

Таблица №2: Исходные данные задачи.

Виды услуг:			1	2	3	№	объём ресурса в	цена ед.
Объёмы оказания услуг:			х1	х2	х3	ресурса	плановый период (ед.)	ресурса
Расход ресурса			4	6	8	1	2400	1	руб.
	на единицу		2	1	3	2	800	2	руб.
	услуги:		1	3	4	3	900	3	руб.
цена услуги:			16	22	32	руб.

Необходимо решить задачу линейного программирования (задачу о распределении неоднородных ресурсов), ответив на следующие вопросы:

1. При каких объёмах использования 3-х процессов получения прибыли (x₁ , x₂ , x_3.), в которых используются 3 вида ресурсов с известными предельными запасами этих ресурсов (b₁ , b₂ , b_3.), прибыль будет максимальна, если расход каждого ресурса и величина прибыли в каждом из процессов линейно зависят от x_i для этого процесса. Для определённости под используемыми процессами получения прибыли будем понимать оказание трёх видов услуг, под объёмом x_i этих процессов будем понимать количество оказанных услуг соответствующего типа.

2. Как будет меняться оптимальный план при изменении b₂ - величины запаса второго ресурса.

3. При каких наименьших ценах на единицу ресурса будет не выгодно дальнейшее оказание услуг за счёт приобретения новых объёмов дефицитных ресурсов.

1) Постановка прямой задачи линейного программирования

Сформулируем теперь прямую задачу ЛП в форме (4) согласно нашим данным. Для этого вычислим величину прибыли, получаемой от оказания единицы каждого вида услуги (т.е. значение коэффициентов с_i из (4) для целевой функции в критерии максимизации прибыли). Эта прибыль есть разность между ценой услуги S_i (последняя строка табл.2) и величиной издержек при её оказании M_i, т.е. суммарной стоимостью ресурсов, расходуемых на единицу этой услуги. Т.е. с_i=S_i-M_i . Величина издержек может быть вычислена по следующей формуле : 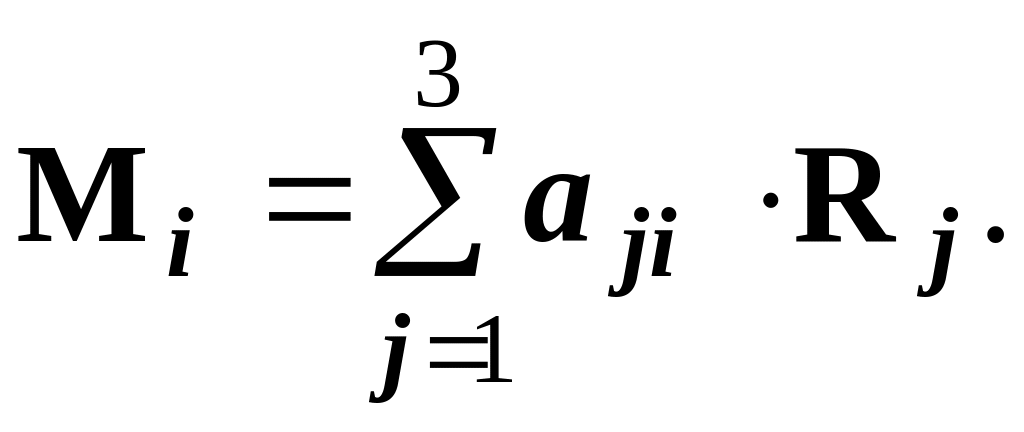Здесь R_j - цена единицы j-го ресурса (последний столбец табл.2). величина издержек и прибыли на одну услугу принимают следующие значения:

M₁= 41+22+13= 11 руб., с₁= 16-11= 5 руб.,

M₂= 61+12+33= 17 руб., с₂= 22-17= 5 руб.,

M₃= 81+32+43= 26 руб., с₃= 32-26= 6 руб.

Теперь можно записать формализованную в форме (4) прямую задачу ЛП:

(11)

2) Исследование модели с помощью дифференциальных коэффициентов ресурсоотдачи

произведём исследование модели с помощью дифференциальных коэффициентов ресурсоотдачи k_ji для понижения размерности задачи. Процедура вычисления k₁₁ выглядит следующим образом – надо первый коэффициент целевой функции разделить на первый коэффициент первого ограничения - k₁₁=с₁/a₁₁=5/4=1,25. Аналогично для k₂₁ – надо первый коэффициент целевой функции разделить на первый коэффициент второго ограничения – k₂₁=с₁/a₂₁=5/2=2,5. В результате матрица коэффициентов К=(k_ji)_33 принимает следующий вид: 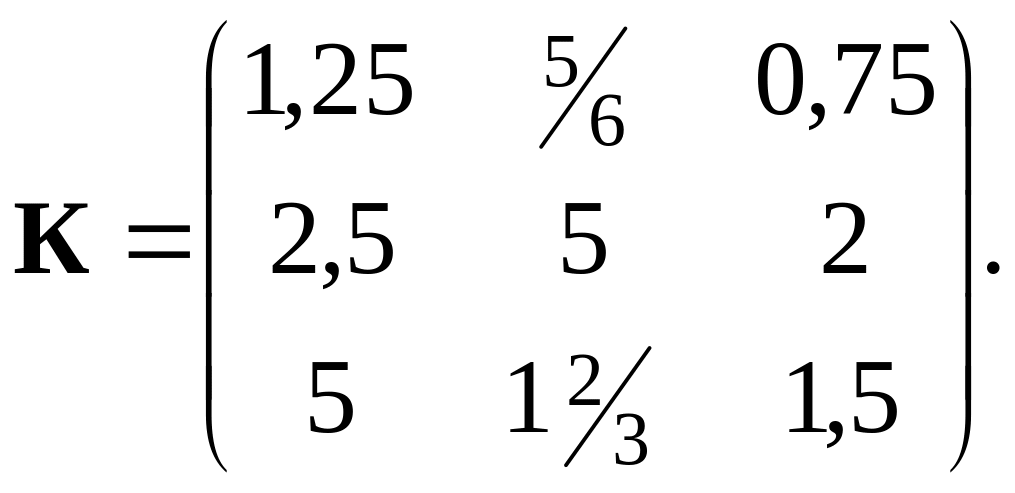Так как все наименьшие по строкам элементы находятся в К в третьем столбце – столбце дифференциальных коэффициентов ресурсоотдачи услуги третьего вида, то использование ресурсов при оказании услуги третьего типа наименее эффективно и в оптимальном плане значение х₃ должно быть равно 0. Таким образом, число переменных в задаче может быть понижено до двух: х₁=х и х₂=у. Такая задача может быть решена графически. Её формализованный вид:

(12)