Алгоритм симплекс-метода

Основным понятием симплекс- метода является симплекс- таблица, которая строится из канонической задачи линейного программирования следующего вида:

В отличие от (6), первая строка (7) – целевая функция – имеет иной вид, к которому, однако, легко преобразовать исходную L(x), положив _i= -c_i , ₀=0. Во второй строке (7) находятся ограничения в форме равенств, в которых присутствуют элементы матрицы , получаемой из упомянутой выше А простым присоединением к ней справа единичной матрицы размера mm: =(АЕ). в задаче (7), аналогично первой части, можно ввести вектор переменных Х размера m+n 1, вектор свободного члена В размера m 1 и вектор коэффициентов целевой функции  размера m+n 1, в котором _i=0 при i>n. Тогда (7) можно записать в матричном виде:

симплекс- таблица строится (см. табл.1) из канонической задачи (7) следующим образом: 1) она содержит n+m+3 столбцов и m+2 строк; 2) первая строка является информационной и содержит заголовки столбцов четырёх типов – столбца имён базисных переменных, столбца их значений в конкретном базовом плане этой симплекс- таблицы, n+m столбцов переменных задачи x_i, столбца контрольных сумм (он не является обязательным и содержит построчные суммы всех числовых значений таблицы); последняя строка называется индексной и содержит параметры ₀,_i целевой функции, а между ними расположены m строк параметров ограничений. Выше было упомянуто, что в симплекс- методе таблица каждой итерации соответствует какой-то вершине МДП. При этом в каждой такой вершине отличны от 0 только m из n+m переменных x_i. Они, как это принято в теории линейных систем, называются базисными, а остальные – свободными. Свободные переменные полагаются равными 0. В симплекс таблице действует следующее правило: базисные переменные перечислены в первом столбце, а их значения в данном базовом плане находятся во втором столбце. Этот план является оптимальным, если симплекс- таблица удовлетворяет критерию оптимальности: индексная строка содержит только положительные и нулевые значения.

Таблица №1. Симплекс- таблица общего вида (для случая исходного заполнения).

Базис	План	х1	х2	…	хn+1	…	хn+m	Контроль
хn+1	b1	a11	a12	…	1	…	0	1
xn+2	b2	a21	a22	…	0	…	0	2
…	…	…	…	…	…	…	…	…
xn+m	bm	am1	am2	…	0	…	1	m
	0	1	2	…	n	…	n+m	m+1

Итеративная процедура симплекс- метода состоит в последовательном преобразовании этой таблицы от одного базового плана к другому в случае возможности улучшения плана. Признаком наличия лучшего, по сравнению с достигнутым, плана является критерий возможности улучшения плана: если индексная строка симплекс- таблицы содержит отрицательные элементы, а в столбцах над ними имеются элементы a_ji, отношение b_j/a_ji для которых больше нуля, то данный план может быть улучшен. Если все отношения b_j/a_ji в столбцах над отрицательными элементами индексной строки меньше нуля или равны  (a_ji=0), то задача не имеет конечного оптимального плана. Это критерий отсутствия оптимального плана. Улучшение плана производится путём введения в состав базисных переменных х_{l –} той переменной, в столбце которой находится наибольшее по модулю отрицательное _l, и выведения из базиса той переменной х_k, для которой отношение b_k/a_kl наименьшее положительное (если положительных нет, то неотрицательное). Столбец таблицы, содержащий х_l , строка таблицы с х_k и элемент a_kl, стоящий на их пересечении, называются ключевыми, или разрешающими. Для упрощения дальнейших уравнений принято ключевой элемент обозначать . Процедура пересчёта всех элементов таблицы называется получением симплекс- таблицы следующей итерации, в ней действуют следующие простые правила: все элементы ключевой строки старой таблицы необходимо разделить на ключевой элемент. элементы всех остальных строк новой таблицы, включая индексную, получаются путём вычитания из соответствующих им элементов симплекс- таблицы предыдущей итерации разделённого на ключевой элемент произведения двух элементов старой таблицы, один из которых стоит на пересечении ключевой строки со столбцом, содержащим пересчитываемый элемент, а другой – на пересечении ключевого столбца и строки, содержащей пересчитываемый элемент. Это преобразование производится по нижеприведённым формулам:

для ключевой k-й строки -

(9)

для остальных строк –

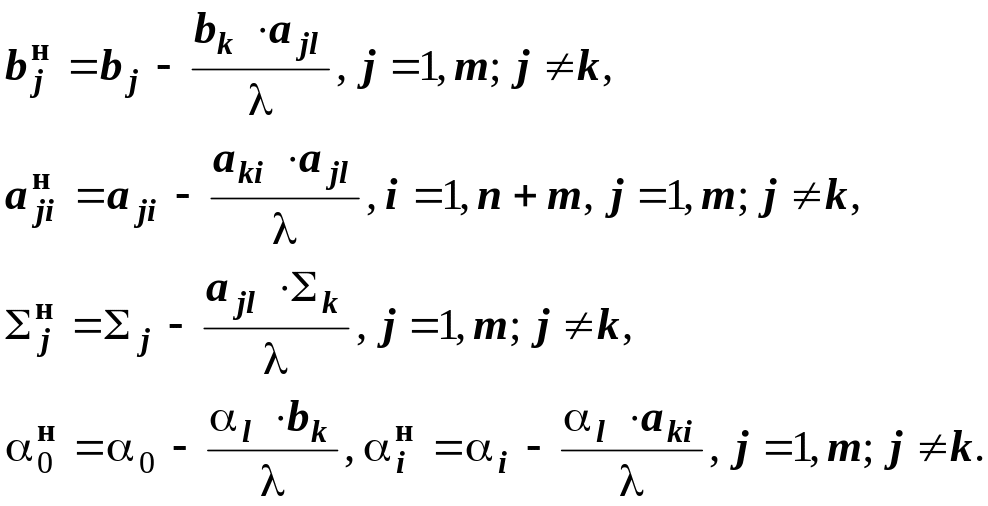(10)

Здесь верхний индекс ^н – признак элемента новой симплекс- таблицы, его отсутствие – признак элемента симплекс- таблицы предыдущей итерации. Элементы столбца контрольных сумм рассчитываются также путём простого суммирования всех остальных элементов соответствующей строки новой таблицы. Верно полученной считается симплекс- таблица, в которой все элементы столбца контрольных сумм одинаковы в обоих подходах к их вычислению – и при суммировании, и по формулам (9), (10). Симплекс- таблица оптимального плана обладает следующими свойствами: отличны от нуля и равны значениям столбца плана только те переменные (х_i, i=1,n) оптимального плана, которые присутствуют в столбце базиса; находящиеся в столбце плана значения дополнительных переменных (х_i, i=n+1, m), присутствующих в столбце плана, это величины остатков не полностью расходуемых ресурсов с номерами i-n. Ненулевые элементы индексной строки делятся на две группы: _i при i>n – это двойственные оценки дефицитных (не полностью расходуемых) в данном оптимальном плане ресурсов с номерами i-n. Т.е. это решение двойственной к исходной задачи! Т.о. симплекс- метод позволяет решать задачи (4) и (5) одновременно. Альтернативной к приведенной при постановке задач (4) и (5) интерпретацией двойственных оценок является тот факт, что эти оценки являются коэффициентами пропорциональности между приращением значения целевой функции оптимального плана и вызвавшими это приращение изменениями запасов ресурсов. То- есть они показывают (грубое объяснение), на сколько увеличится значение целевой функции исходной задачи в оптимальном плане при увеличении величины соответствующего двойственной оценке запаса ресурса на единицу. Т.о., двойственные оценки – приростные коэффициенты ресурсоотдачи. Вторая группа _i при in имеет менее полезное с экономической точки зрения значение – это величина превышения издержек оказания единицы не включённых в оптимальный план видов услуг с номером i над их ценой при условии расчёта издержек с использованием в качестве цен ресурсов их двойственных оценок. Во всяком случае, можно отметить следующее свойство – не равны нулю элементы индексной строки, соответствующие невыгодным (не включённым в оптимальный план) видам услуг или продукции и дефицитным ресурсам. В случае невыполнения этих требований при преобразованиях симплекс- таблицы были допущены ошибки.