5. Подпространства линейных пространств. Линейные оболочки.

Определение 1. Подпространством линейного пространства L называется такое подмножество

элементов L, которое само является линейным пространством.

Т.е. подпространство замкнуто относительно операций сложения и умножения на число. (все аксиомы выполняются автоматически).

Примеры. , множество решений однородной СЛАУ.

Определение 2. Линейной оболочкой системы элементов , принадлежащих L , называется совокупность всех линейных комбинаций этих элементов: .

Непосредственно из определения следует, что любая линейная оболочка является линейным пространством, а любое линейное пространство – линейной оболочкой натянутой на какой-либо базис этого пространства.

Теорема 1 (основное свойство линейных оболочек). Любой вектор системы , линейно зависящий от остальных, можно исключить без изменения линейной оболочки.

{Пусть, для определенности, а произвольный . Тогда

, т.е. }

Следствие. Размерность линейной оболочки равна рангу соответствующей системы элементов:

 

6. Переход к новому базису.

Пусть {e₁,…,e_n} и {f₁,…,f_n} - 2 базиса в линейном пространстве L. Первый будем считать исходным, а второй – новым. Все векторы нового базиса разложим по векторам исходного: , или в матричной форме записи (f₁,…,f_n) =(e₁,…,e_n)А, или , где 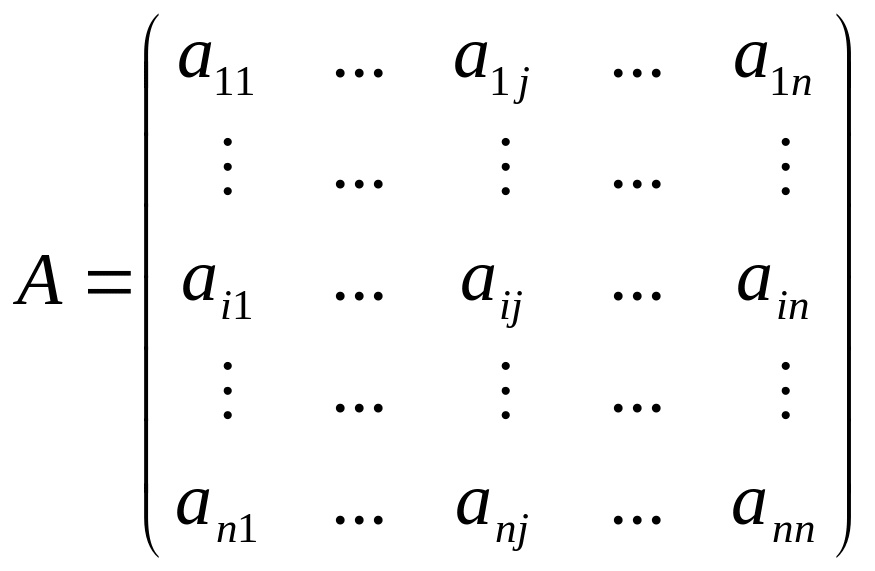− матрица перехода от базиса {e_i} к базису {f _j}, столбцами которой являются координаты векторов f_j в базисе {e_i}.

Так как, по условию, столбцы матрицы A линейно независимы, ее определитель не равен нулю и она имеет обратную. Следовательно, переход от базиса {f _j} к базису {e_i} можно осуществлять по формуле (e_i)=(f _j)А^-1.

Пусть b – произвольный элемент из L. В базисе {e_i} он равен: , или, в матричной форме: b=(e₁,…,e_n)(b₁,…,b_n)^т.

Соответственно, в базисе {f _j} имеет место равенство b=(f₁,…,f_n)(₁,…,_n)^т.

Отсюда: (e₁,…,e_n)(b₁,…,b_n)^т =(f₁,…,f_n)(₁,…,_n)^т.

Подставляя {f₁,…,f_n} из формулы перехода, получим: (e₁,…,e_n)(b₁,…,b_n)^т=(e₁,…,e_n)А(₁,…,_n)^т.

Т.к. b произвольный вектор L , имеем:

(b₁,…,b_n)^т =А(₁,…,_n)^т _- формула пересчета новых координат в старые и

(₁,…,_n)^т =А^-1(b₁,…,b_n)^т _- формула пересчета старых координат в новые.

Таким образом, для вычисления столбца координат (x)_{f} в новом базисе приходится решать СЛАУ со столбцом старых координат (x)_{e} в правой части: A (x)_{f}=(x)_{e}

7. Евклидовы пространства.

Определение 1. Линейное пространство E = {f, g, h, …} называется евклидовым, если

ставится в соответствие число, называемое скалярным произведением: . При этом, для выполняются аксиомы:

Имеет место

Неравенство Коши – Буняковского – Шварца:

{ }

По определению, длиной элемента называется: , а косинусом угла между двумя элементами: (В силу неравенства К – Б – Ш это определение корректно)

Отсюда легко получить, что

Примеры. 1)

Определение 2. Линейное пространство N называется нормированным, если N ставится

в соответствие число , называемое нормой элемента , и удовлетворяющее условиям:

Свойство (3) называется неравенством треугольника, а норма есть обобщение понятия ‘длина’.

Примеры. 1) Абсолютная норма:

2)Средняя или евклидова норма:

В нормированных евклидовых пространствах косинус угла между векторами обычно записывают в виде