Государственное образовательное учреждение

высшего профессионального образования

Поволжский государственный университет

телекоммуникаций и информатики

Кафедра Программное обеспечение и управление в технических системах

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к контрольной работе по дисциплине

«ЧИСЛЕННЫЕ МЕТОДЫ»

для студентов заочной формы обучения

САМАРА, 2012 Г.

СОДЕРЖАНИЕ

1.Теоретическая часть 3

1.1 Точные методы 3

1.1.1 Метод Гаусса 3

1.1.2 Связь метода Гаусса с разложением матрицы на множители. Теорема об LU разложении. 5

1.1.3 Метод Гаусса с выбором главного элемента 7

1.1.4 Метод Холецкого (метод квадратных корней) 8

2. Практическая часть 9

2.1 Задание на контрольную работу 9

2.2 Варианты заданий 9

2.3 Пример решения задачи 12

2.4 Требования к оформлению контрольной работы 21

Список использованной литературы 23

1.Теоретическая часть

Решение систем линейных алгебраических уравнений

Рассмотрим систему линейных алгебраических урав­нений:

(1.1)

или в матричной форме:

Aх=b, (1.2)

где: A={a_ij} квадратная матрица размерности (mm,); х=(х₁,…., х_m)^T; T – операция транспонирования; b=(b₁,….,b_m)^T; detA0.

Предположим, что определитель матрицы A не равен нулю. Тогда решение х существует и единственно. На практике встречаются системы, имеющие большой поря­док. Методы решения системы (1.1) делятся на две группы:

1) прямые (точные методы);

2) итерационные методы (приближенные).

1.1 Точные методы

В точных методах решение х находится за конечное число действий, но из-за погрешности округления и их накопления прямые методы можно назвать точными, только отвлекаясь от погрешностей округления.

1.1.1 Метод Гаусса

Вычисления с помощью метода Гаусса (который называют также методом последовательного исключения неизвестных) состоят из двух основных этапов: прямого хода и обратного хода. Прямой ход метода заключается в последовательном исключении неизвестных из системы для преобразования ее к эквивалентной системе с треугольной матрицей. На этапе обратного хода производят вычисления значений неизвестных. Рассмотрим простейший вариант метода Гаусса, называемый схемой единственного деления.

Прямой ход метода

1-й шаг. Предположим, что а₁₁0. Поделим первое уравнение на этот элемент, который назовем ведущим элементом первого шага :

. (1.3)

Остальные уравнения системы (1.1) запишем в виде

, (1.4)

где i= .

Уравнение (1.3) умножаем на a_i1 и вычитаем из i-го уравнения системы (1.4). Это позволит обратить в нуль коэффициенты при x₁ во всех уравнениях, кроме первого.

Получим эквивалентную систему вида:

. (1.5)

,

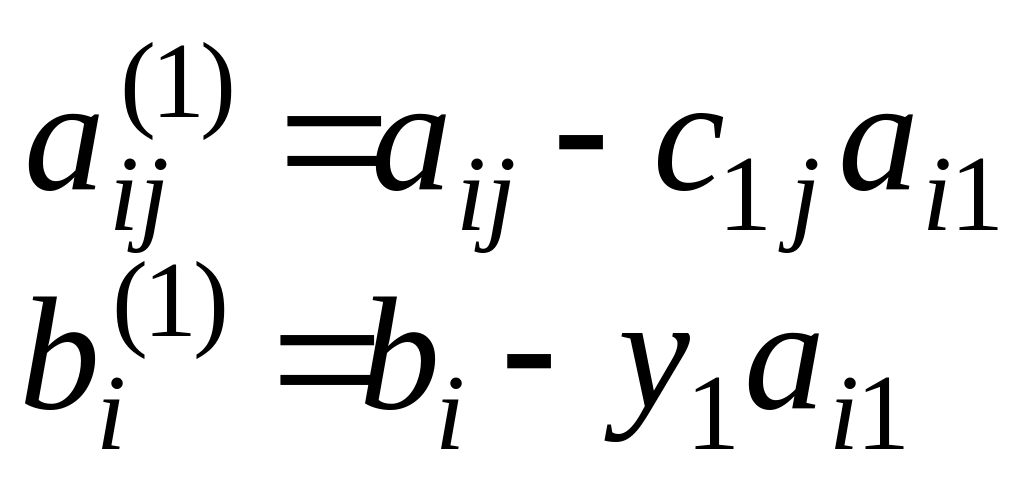где i,j= . Система (1.5) имеет матрицу вида:

.

Дальше работаем с укороченной системой, т.к. х₁ входит только в 1-ое уравнение

.

2-й шаг. На этом шаге исключаем неизвестное х₂ из уравнений с номерами i=3,4,…,m. Если ведущий элемент второго шага , то из укороченной системы ана­логично исключаем неизвестное x₂ и получаем матрицу коэффициентов такого вида:

.

Аналогично повторяем указанные действия для неиз­вестных х₃,х₄,...,х_m-1 и приходим к системе :

. (1.6)

Эта система с верхней треугольной матрицей:

.

Обратный ход метода. Из последнего уравнения сис­темы (1.6) находим х_m, из предпоследнего х_m-1, ..., из пер­вого уравнения – х₁.

Общая формула для вычислений:

x_m=y_m/c_mm,

, (i=m-1,…,1).

Для реализации метода Гаусса требуется примерно (1/3)m³ арифметических операций, причем большинство из них приходится на прямой ход.

Ограничение метода единственного деления заключа­ется в том, что ведущие элементы на k-ом шаге ис­ключения не равны нулю, т.е. ≠0.

Но если ведущий элемент близок к нулю, то в процессе вычисления может накапливаться погрешность. В этом случае на каждом шаге исключают не х_k, a х_j (при jk). Такой подход называется методом выбора главного элемента. Для этого выбирают неизвестные x_j с наибольшим по абсолютной величине коэффициентом либо в строке, либо в столбце, либо во всей матрице. Для его реализации требуется − арифметических действий.