МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Сыктывкарский лесной институт (филиал) федерального государственного

бюджетного образовательного учреждения высшего профессионального

образования «Санкт - Петербургский государственный

лесотехнический университет имени С. М. Кирова»

(СЛИ) 

 

 

 

 

Отчет

Лабораторные работы по ТММ

 

 

Выполнили: Морохин В.О.

Специальность:АС

Курс: 3

Форма обучения: очная

Проверил: Сухоруков И.Н.

 

 

 

 

 

 

 

 

Сыктывкар 2014

Лабораторная работа №1

Определение основных параметров зубчатых колес с помощью инструментов

Цель работы: определение основных размеров зубчатых колес.

Задачи работы: 1. Измерение размеров зубчатого колеса.

2. Определение модуля и основных параметров.

Обеспечивающие средства:зубчатое колесо, штангенциркуль, калькулятор, чертежныеинструменты.

Теоретическая часть

На рис. 1 и 2 показаны основные параметры зубчатого колеса.

Рис. 1. Зубчатое колесо	Рис. 2. Зуб колеса

Основные параметры зубчатого колеса:

z – число зубьев;

m_t– модуль зацепления;

d – диаметр делительной окружности;

d_b– диаметр основной окружности;

б – угол зацепления;

P_t– шаг зацепления;

d_a– диаметр окружности выступов (головок);

d_f– диаметр окружности впадин (ножек);

S_t– толщина зуба по дуге делительной окружности;

S_tx– толщина зуба по хорде делительной окружности;

h_a– высота головки зуба;

h_f– высота ножки зуба.

Модуль зацепления колеса с эвольвентным профилем зуба может быть определен на основании следующего свойства эвольвентного зацепления: «Нормаль, проведенная в любой точке соприкасающихся эвольвентных профилей, является касательной к основной окружности». Если измерить расстояние между зубьями по нормали, то это будет шаг зацепления по основной окружности. 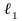Для этого необходимо штангенциркулем измерить расстояния и . При этом, чтобы измерение происходило по нормали, число зубьев 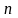для должно соответствовать значению табл. 1, в зависимости от общего числа зубьев .

Таблица 1

z	12-18	19-27	28-36	37-45	46-54	55-63	64-72
n	2	2	4	5	6	7	8

При измерении штангенциркулем охватывается на один зуб больше:

Шаг зацепления по основной окружности:

Модуль зацепления определяется по формуле:

где – угол зацепления, равный 20^.

Полученное значение модуля необходимо уточнить, округляя до ближайшего стандартного значения (табл. 2).

Таблица 2

Стандарт нормальных модулей по ГОСТ 1597

Величина модуля, мм	Интервал, мм
от 0,3 до 0,8	0,1
от 1,0 до 4,5	0,25
от 4,5 до 7,0	0,5
от 7,0 до 16,0	1,0
от 18 до 30	2,0
от 33 до 45	3,0
от 45 и выше	5,0

Правильность определения модуля проверяется формулой:

где 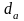– диаметр окружности выступов, который измеряется штангенциркулем непосредственно при четном числе z или косвенно при нечетном числе z.

При несовпадении значений модуля, полученных по формулам, необходимо повторить замеры.

Для колес, нарезанных с нулевым сдвигом, основные параметры определяются по следующим формулам:

диаметр делительной окружности:

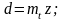
диаметр основной окружности:

диаметр окружности выступов (головок):

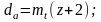
диаметр окружности впадин (ножек):

высота головки зуба:

высота ножки зуба:

шаг зацепления:

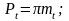
толщина зуба по дуге делительной окружности:

толщина зуба по хорде делительной окружности:

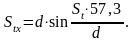
Величин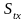у можно непосредственно измерить штангенциркулем (рис. 2). Для этого предварительно вычисляют величину:

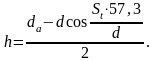
Практическая часть

1. Число зубьев –Z = 23;

2. l₁=28 мм, l₂=46 мм.

Шаг зацепления по основной окружности: Р_t^b=l₂-l₁=46-28=18 мм

3. Модуль зацепления:

m_t= Р_t^b/(π·cosα) = 18/(3,14·cos20) = 6 мм

По таблице 2 определяем интервал, т.к величина модуля 6,1, то интервал 0,5

4. d_a = 150 мм - диаметр окружности выступов, который измеряется штангенциркулем непосредственно при четном числе z или косвенно при нечетном числеz.

Правильность определения модуля проверяется формулой:

m_t = d_a/(Z+2) = 150/(23+2)=6

5. Для колес, нарезанных с нулевым сдвигом, основные параметры определяются по следующим формулам:

• диаметр делительной окружности:

d=m_t·Z = 6·23=138 мм;

• диаметр основной окружности:

d_b = d·cosα = 138·cos20 = 129,7мм;

• диаметр окружности выступов (головок):

d_a = m_t·(Z+2) = 6·(23+2) = 150 мм;

• диаметр окружности впадин (ножек):

d_f = m_t·(Z-2,5) = 6·(23-2,5) = 123 мм;

• высота головки зуба:

h_a = (d_a - d)/2=(150 - 138)/2 = 6 мм;

• высота ножки зуба:

h_f = (d - d_f)/2 = (138-123)/2 = 7,5 мм;

• шаг зацепления:

P_t = π·m_t = 3,14·6 = 18,8 мм;

• толщина зуба по дуге делительной окружности:

S_t = P_t/2 = (π·m_t)/2 = 9,4 мм;

• толщина зуба по хорде делительной окружности:

S_tx= d·sin[(S_t·57,3)/d] = 138·sin[(9,4·57,3)/138] = 9,4мм.

6. Замерить d_aи , d_f: d_a = 150 мм, d_f = 123 мм. Замеренноеd_a и d_f совпадают с расчетными значениями.

Вывод к работе:определили основные параметры зубчатых колес: число зубьев, модуль зацепления, диаметр делительной окружности, шаг зацепления.

Лабораторная работа №2 Кинематический анализ зубчатых механизмов

Цель работы: освоить проведение кинематического исследования зубчатых механизмованалитическим и опытным методами.

Задачи работы:

1. Составить по модели кинематическую схему зубчатого механизма.

2. Вычислить число степеней свободы зубчатого механизма по П. Л. Чебышёву.

3. Вычислить передаточное отношение зубчатого механизма аналитическим и экспериментальным методом.

4. Определить погрешность экспериментального метода в сравнении с аналитическим.

Обеспечивающие средства: модели зубчатых механизмов, чертежные инструменты,калькулятор.

Теоретическая часть

Передаточное отношение является основным кинематическим параметром зубчатых механизмов. Согласно ГОСТ 16530-83 передаточным отношением называется отношение угловых скоростей звеньев (или частоты вращения), т.е. г де ω1 — угловая скорость ведущего звена,

ω2 — угловая скорость ведомого звена механизма.

Зубчатая передача- трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими со стойкой вращательные пары.

Зубчатое зацепление- кинематическая пара, образованная зубчатыми колесами передачи.

Блок зубчатых колес- звено, образованное несколькими, жестко связанными между собой зубчатыми колесами с общей осью вращения. Сложные зубчатые механизмы делятся на ряды и планетарные механизмы.

Ряд зубчатых колес- механизм, все зубчатые колеса которого вращаются вокруг неподвижных осей.

Планетарный зубчатый механизм- механизм , в состав которого входят зубчатые колеса с подвижными осями вращения.

Степень подвижности зубчатых механизмов можно определить по формуле Чебышева:

W=3n-2р₅-р₄ ,

где n-число подвижных звеньев

р₄, р₅-кинематические пары с одной и с двумя наложенными связями.

Практическая часть

Порядок выполнения работы:

1. Составить кинематическую схему механизма.

2. Посчитать степень подвижности механизма по формуле Чебышева.

3. Определить тип зубчатого механизма.

4. Подсчитать число зубьев колес и вычислить передаточное отношение механизмов.

5. Проверить передаточное отношение механизма путем измерения углов поворота ведущего и ведомого звеньев.

1. Механизм с неподвижными осями с эвольвентным зацеплением конической и цилиндрической формы.

Z₁ = 25

Z₂ = 25

Z₃ = 75

Z₄ = 100

W = 3n – 2p₅ – p₄ = 3·3 - 2·3 -2 = 1 – степень подвижности

Передаточное отношение каждой пары:

i₁₂ = Z₂/Z₁ = 25/25 = 1

i₃₄ = Z₄/Z₃ = 100/75=1,3

i₁₄ = i₁₂·i₃₄ = 1·1,3 = 1,3

i₁₄ = φ₁/ φ₂ = 1,3

2. Механизм с подвижными осями с эвольвентным зацеплением цилиндрической формы.

Z₁ = 60

Z₂ = 58

Z₃ = 62

Z₄ = 56

W = 3·3 - 2·3 – 2 = 1 – степень подвижности

Передаточное отношение:

Вывод к работе: передаточное отношение, вычисленное расчетным путем равно передаточному отношению, измеренному экспериментальным путем.