Лекция 5 Транспортные задачи. Основные понятия Формулировка транспортной задачи. Математическая модель

Задача: Однородный груз, имеющийся в m пунктах отправления (производства) в количествах а₁, а₂, ..., а_m единиц, требуется доставить в каждый из n пунктов назначения (потребления) в количествах b₁, b₂ ..., b_n единиц. Стоимость перевозки (тариф) единицы продукции из i-ого пункта отправления в j-ый пункт назначения составляет c_ij (i=1, …, m; j=1, …, n). Требуется составить такой план перевозок, при котором весь груз из пунктов отправления вывозится, и запросы всех пунктов потребления удовлетворяются

Исходные данные ТЗ записываются в таблице:

ПН ПО	1		2		…	n		Запасы
1		c11		c12	…		c1n	a1
2		c21		c22	…		c2n	a2
…	…		…		…	…		…
m		cm1		cm2	…		cmn	am
Потреб- ности	b1		b2		…	bn

Пусть x_ij – количество груза перевозимого с i-ого пункта отправления (ПО) в j-ый пункт назначении (ПН). Матрица 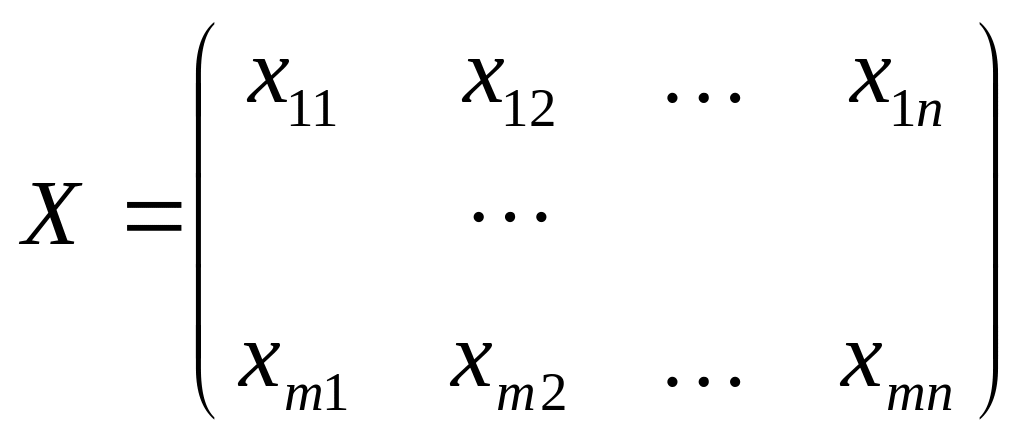– план перевозок.

Произведение c_ijx_ij определяет затраты на перевозку груза с i-ого ПО в j-ый ПН. Тогда суммарные затраты на перевозку груза равны . По условию задачи необходимо обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид

.

Так как груз из всех m пунктов отправления вывозиться полностью, то

.

Так как запросы всех n пунктов назначения удовлетворяется полностью, то

.

По смыслу плана x_ij0, (i=1,…,m; j=1,…,n)

Следовательно, математическая модель транспортной задачи имеет вид:

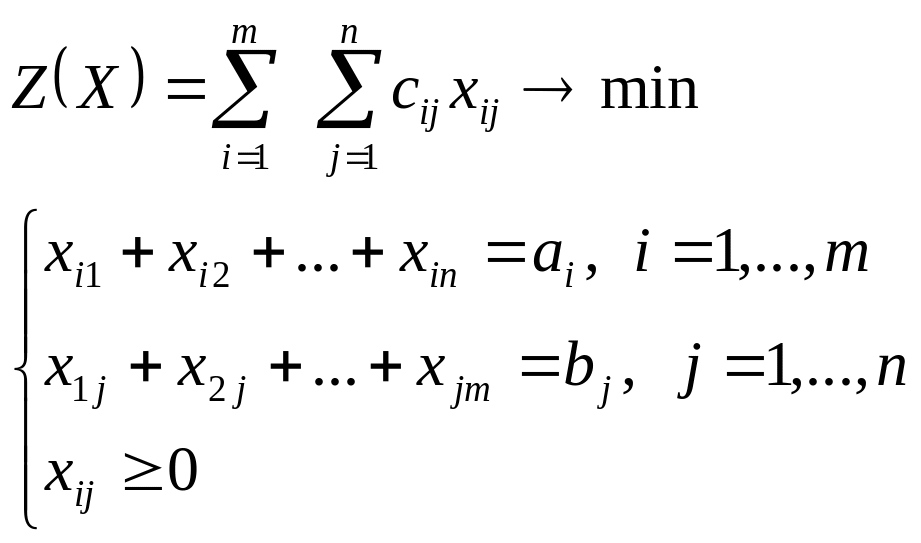. (1)

Замечание. В транспортной задаче m+n уравнений и mn неизвестных.

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.

(2)

Такая задача называется задачей с правильным балансом, а ее модель – закрытой. Если равенство (2) не выполняется, т.е. , то задача называется задачей с неправильным балансом, а ее модель – открытой.