9.Өлшеу нәтижелерін және кездейсоқ қателердің математикалық күтімі мен дисперсиясын сипатаңдар.

Дифференциалдық – интегралдық таралу функциялары ыңғайлы болып табылады, бірақ анықтау өте қиын жұмыс. Сондықтан көп жағдайда толық функцияны анықтаудың орнына моменттер деп аталады. Кейбір маңызды нүктелерді анықтау жеткілікті болады.

2. түрі бар: 1)бастапқы

2)орталық мометтер

Бастапқы моменттің жалпы теңдеуі:

r=1 α₁[x]=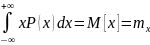

математикалық күтімі дейді. Жүйелік қате жойылғанда математикалық күтімді шаманың шын мәнінде алуға болады. Q=m[x]-Q Q-жүйелі қате

Q=0 болса, M[x]=Q

Ал кездейсоқ қате δ=х-M[x]. Шын мәнінің орнына математикалық күтімді аламыз: δ=0 болса, X=M[x].

Орталық момент

M_r[x]= 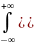- M_x)* ^rP(x)dx

M_x-математикалық күтім

r=1 M₁[x]= - M_r)* ^rP(x)d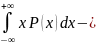x= M_x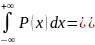 M_x-M_x=0

бірінші орталық момент 0 тең.

Біз үшін маңыздысы екіншісі орталық момент: r=2 M₂[x]=D[x]=D[δ]

Өлшенетін шаманың дисперсия мен кездейсоқ шамаларының декарттары өзара тең болады.

M₂[x]=D[x]=D[δ]= -m₂)²P(x)dx= ²P(x)dx

Осы интегралды дисперсия деп аталады.

Дисперсия – кездейсоқ шаманың мәндерінің шашырауын көрсетеді.

Квадрат ыңғайлы болмағандықтан, көбіне оның түбір асты мәнін алады: δ_x=+

Осыны орташа квадраттық ауытқу деп аталады

10.Нүктелі бағалау

Х₁ ,х_2, х₃...х_n сұраптау осы нәтижелерге сүйене отырып шын мәнін бағалауымыз керек.

Сұрыптау:

1.жалпы негізгі сұрыптау

2. тәжірибелік сұрыптау

Нүктелі бағалауда бағаланатын шаманы 1 ғана санмен бағалайды.

Бағалау бірнеше талаптарға сәйкес болу керек:

1. Өлшем саны n өскен сайын бағалау шын мәніне жуықтау керек.

2. Егер жүйелі қате жойылған болса, онда өлшенетін шама мәні ретінде математикалық күтімге тең деп аламыз.

3. Барлық бағалаудың арасында дисперциясы ең кем болатын бағалау басқа бағалаулардан жақсы болады.

Фишер принципі. Шын мәніне ең жуықтау принципі.Р(х, Q, )

1.Гаусс таралуы.

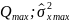мәні бағалау мәні ретінде алынады.

Өлш-н шама-ң шын мәніне бағалауы:

= орташа арихметикалық мән

Дисперция

=1/n·∑(х_і - )²

Өлшенетін шама бағалау: =1/n·∑х_і

S_х² =1/n-1·∑(х_і - )²

S_х=√1/n-1·∑(х_і - )² – орташа квад-қ ауытқу

S_х-² =(1/n) * (1/n-1) ·∑(х_і – )²

Лаплас таралуындағы өлшенетін шама

Ƴ=∑│ х_і - │-мин мәнге жетсе, сол Q бағаланатын шама болады.

₁=1/n∑ х_і

Біркелкі таралу

= =

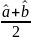
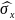11.Аралық бағалау

Нүктелік бағалауды бірінші сатысы ретінде қарастыру керек. Бұдан ары дамытуды аралық бағалау деп атайды.

Аралық бағалауда бағаланатын шаманың белгілі шекаралары мен шектелген аралықта жату ықтималдығын анықтайды.

Осы ықтималдықты сенімді ықтималдық дейді, ал шекараларды сенімді шекаралар дейді.

; P=0,95;

;

;

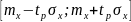
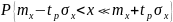
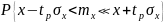
P=0,95; P=