10.2.4. Доверительные интервалы для параметров и функции регрессии

На основе статистики ti получаем доверительный интервал для параметра

i , i 1,m:

i t1 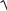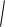12ai,i i i t1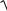 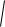12ai,i .

На основе статистики ty получаем доверительный интервал для истинного зна-

чения функции регрессии y HT :


			2	H	T		A	1					2	H	T	A	1	H .
y t1		1		H			A			H y y t1		1		H		A		H .
	2										2
В этих выражениях t	1		100			1			-процентное отклонение распределения T
В этих выражениях t			100						-процентное отклонение распределения T
							2												n m
	2						2
	2

(Стьюдента с n m степенями свободы).

На основе статистики v получаем доверительный интервал для дисперсии

							2				2			2
				(n m) 1							2	(n m) 1			,
					v1							v1			,
					v1							v1
						2							2
где v1 ,	v1	– 100	1		- и 100			1		-процентные отклонения распределения
где v1 ,	v1	– 100			- и 100					-процентные отклонения распределения
		2							2
2	2	2							2
2	2
Hn m (хи-квадрат с n m степенями свободы).
Статистики		ti , v можно использовать для проверки гипотез о параметрах

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 2829 / 3229 30 31 32 > Следующая >>>