Добавил:

Kaz Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет информатики и радиоэлектроники

Предмет:

Структуры и алгоритмы обработки данных

Файл:

СМОД – Статистические методы обработки данных / Муха, Слуянова, БГУИР 2004 (Лаб практикум).pdf

Скачиваний:

Добавлен:

15.06.2014

Размер:

708.82 Кб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3219 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

ЛАБОРАТОРНАЯ РАБОТА № 7. ПОЛУЧЕНИЕ ИНТЕРВАЛЬНЫХ

ОЦЕНОК ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ

7.1.Цель работы

7.1.1.Изучение задачи получения интервальных оценок параметров распре-

делений.

7.1.2. Приобретение навыков получения интервальных оценок параметров

распределений в системе Matlab.

7.2. Теоретические положения

Интервальные оценки параметров распределений

Доверительным интервалом для некоторого параметра	называется интер-
вал ( н, в ), накрывающий параметр с доверительной вероятностью :
P( н в ) .	(7.1)

Задача получения интервальной оценки параметра распределения заключа-

ется в определении по выборке (x1,x2,..., xn ) нижней и верхней границ интер-

вала н , в . Доверительная вероятность выбирается близкой к 1 из набора чи-

сел {0,9; 0,95; 0,975}.

Для придания задаче однозначности уравнение (7.1) представляют в виде

двух уравнений

	P( в ) 1,	(7.2)
		(7.2)
	P( н ) 2,
где 1 2	1 .
Доверительный интервал называется симметричным, если		в (7.2)

1 2 (1 )/2. Таким образом, симметричный доверительный интервал удовлетворяет следующей системе уравнений:

		1
P(	в )		,
P(	в )	2	,
		2	(7.3)
		1	(7.3)
		1
P(	н )			.
P(	н )	2		.
		2

Для построения симметричного доверительного интервала для неизвестного

параметра обычно используется статистика, представляющая собой точеч-

ную оценку этого параметра, или некоторая функция точечной оценки

g g( ). Должен быть известен закон распределения этой статистики, то есть плотность вероятности fg (x). В силу того что параметр нам неизвестен, эта плотность вероятности будет зависеть от , то есть нам известна плотность ве-

роятности статистики с точностью до параметра fg (x, ). Для построения до-

верительного интервала для параметра строят «доверительный интервал» для статистики g, то есть находят gн , gв из системы уравнений

		1
P(g g	в )		,
		2

		1

P(g g	н )			.

		2

Решение этой системы уравнений относительно gн , gв эквивалентно решению системы уравнений (7.3) относительно н , в .

Приведем доверительные интервалы для некоторых параметров.

7.2.1. Доверительный интервал для математического ожидания a нор-

мальной генеральной совокупности N(a, 2 ) при известной дисперсии 2

xu12 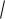n a x u12 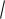n ,

где

x 1 n xi , n n 1

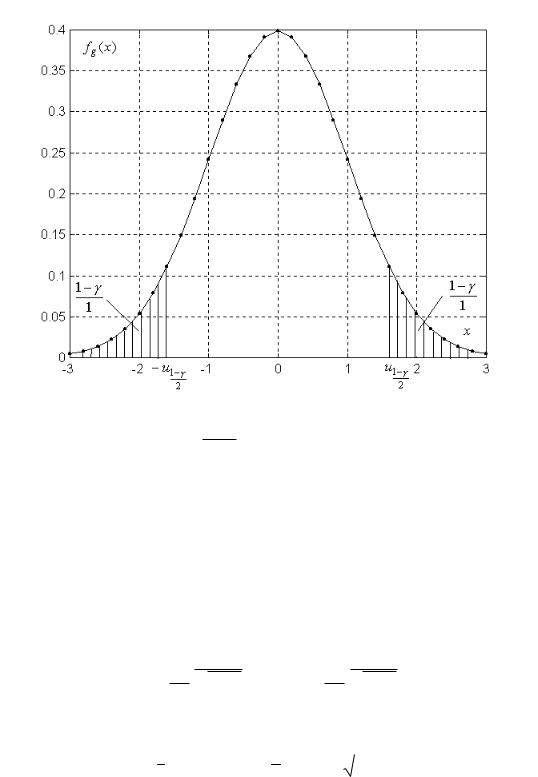
u1	– 100	1	-процентное отклонение нормального распределения N(0,1)

	2
2

(рис. 7.1).

Рис. 7.1. Иллюстрация 1001 -процентного отклонения нормального

распределения

7.2.2. Доверительный интервал для математического ожидания a нор-

мальной генеральной совокупности N(a, 2 ) при неизвестной дисперсии

x t12 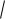n 1 a x t12 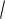n 1,

где

		1		n

s	2			(xi	x	)2,	s s2 ,

			n n 1

t	1		– 100			1			-процентное отклонение																			распределения T (n 1). В силу сим-
t			– 100						-процентное отклонение																			распределения T (n 1). В силу сим-
					2																								1
	2				2
	2
метричности распределения Стьюдента																												T1(n 1) величина									t1 имеет ту же
																																						2
графическую иллюстрацию, что и величина u1 (рис. 7.1).
																																	2
		7.2.3. Доверительный интервал для дисперсии 2																																			нормальной гене-
ральной совокупности												N(a, 2 )											при					известном математическом ожида-
нии a
																ns02											2			ns02
																																			,
																v1																			,
																v1														v1
																		2													2
где
																						1			n
															s02										(xi				a)2,
															s02										(xi				a)2,
																								n n 1
v1 ,v1					– 100				1	- и 100				1			-процентные отклонения распределения H1(n)
v1 ,v1					– 100					- и 100							-процентные отклонения распределения H1(n)
								2				2
	2	2						2				2
	2	2
(рис. 7.2).
		7.2.4. Доверительный интервал для дисперсии 2																																			нормальной гене-
ральной совокупности N(a, 2 )																						при неизвестном математическом ожида-
нии a
																ns				2							2			ns				2		,
															w1																					,
															w1														w1
																			2													2
где			w		,w			– 100			1		- и 100								1					-процентные отклонения распределения
где			w		,w			– 100					- и 100													-процентные отклонения распределения
			1			1		2														2
				2			2	2														2
				2			2
H1(n 1)					(рис. 7.2).

Рис. 7.2. Иллюстрация 1001 - и 1001 -процентных отклонений

2 2

распределения хи-квадрат

7.2.5. Доверительный интервал для вероятности появления случайного

события A

Пусть выполнено n независимых испытаний Бернулли, в результате кото-

рых событие А появилось m раз. Границы доверительного интервала для веро-

ятности p P(A) события A определяются выражением
							2
							2						2
				n			u1						u1
				n				2				pq		2	,
						p				u	1
				n u	2		2n				1	n	4n2
				n u	2		2n					n	4n2
					1				2
					2
где u1 100		1	-процентное отклонение распределения												N(0,1), p p	m	–
где u1 100			-процентное отклонение распределения												N(0,1), p p		–
	2															n
2	2															n
2

частота события, q 1 p. При знаке минус эта формула дает нижний довери-

тельный предел, а при знаке плюс – верхний.

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3219 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в папке СМОД – Статистические методы обработки данных

#
15.06.2014708.82 Кб98 Муха, Слуянова, БГУИР 2004 (Лаб практикум).pdf
#
15.06.2014175.21 Кб58laba_1.docx
#
15.06.2014757.86 Кб56laba_2.docx
#
15.06.2014142.13 Кб61laba_3.docx
#
15.06.2014628.44 Кб64laba_5.docx
#
15.06.20140 б60Лаба 1 Нормальное и равномерное распределение.txt