- •Методические указания по выполнению контрольной работы по дисциплине «Элементы высшей математики»
- •Для специальности 230115 «Программирование в компьютерных системах»
- •Оглавление
- •2.3.2 Раскрытие неопределенности типа
- •2.3.3 Раскрытие неопределенности типа .
- •Раздел 5. Неопределённый интеграл.
- •Пояснительная записка
- •Раздел 1. Определители и матрицы. Решение систем линейных уравнений
- •Основные понятия и определения
- •1.2 Вычисление определителей 2-го порядка.
- •1.3 Миноры и алгебраические дополнения элементов определителя.
- •1.4 Вычисление определителей 3-го порядка.
- •1.5 Матрицы. Основные понятия и определения
- •1.6 Виды матриц.
- •1.7 Элементарные преобразования матриц.
- •1.8 Системы n линейных уравнений с n неизвестными. Основные понятия и определения
- •1.9 Метод Крамера решения систем линейных уравнений.
- •1.10 Метод Гаусса решения систем линейных уравнений.
- •Раздел 2 предел функции.
- •2.1 Определение предела функции
- •2.2 Основные теоремы о пределах функции.
- •2.3 Вычисление пределов функций.
- •2.3.1 Раскрытие неопределенности типа
- •2.3.2 Раскрытие неопределенности типа
- •II в числителе или (и) в знаменателе дроби присутствует иррациональность.
- •III в предельном выражении присутствуют тригонометрические функции.
- •I специальный (замечательный) предел
- •2.3.3 Раскрытие неопределенности типа .
- •Раздел 3. Производная. Правила дифференцирования. Таблица производных элементарных и сложных функций.
- •3.1Задача, приводящая к понятию производной. Определение производной.
- •Задача о мгновенной скорости.
- •Определение производной функции.
- •3.3 Основные правила дифференцирования.
- •Производная постоянной величины.
- •3. Производная произведения.
- •Производная сложной функции
- •3.4 Таблица производных элементарных функций.
- •3.5 Таблица производных сложных функций
- •3.6 Приложение производной к вычислению пределов функций.
- •Раздел 4 приложения производной. Приложения производной к исследованию функций и построению графиков.
- •4.1. Интервалы монотонности функции
- •4.2 Экстремумы функции
- •4.3 Интервалы выпуклости и вогнутости графика функции. Точки перегиба.
- •4.4 Асимптоты графика функции
- •4.5 Общая схема исследования функции и построение её графика
- •Раздел5. Неопределённый интеграл.
- •5.1. Неопределённый интеграл: основные понятия, определения, свойства
- •5.4.1 Непосредственное интегрирование.
- •5.4.2. Метод замены переменной (способ подстановки).
- •Интегрирование по частям.
- •Раздел 6. Определённый интеграл.
- •6.1. Определённый интеграл: основные понятия, определения, свойства.
- •6.2 Свойства определённого интеграла.
- •6.3. Формула Ньютона - Лейбница. Основные методы вычисления определённого интеграла.
- •6.3.1 Непосредственное интегрирование.
- •6.4. Геометрические приложения определенного интеграла.
- •Раздел 7. Комплексные числа.
- •7.1. Понятие комплексного числа, алгебраическая форма записи комплексного числа. Действия с комплексными числами в алгебраической форме.
- •7.3 Геометрическое изображение комплексного числа.
- •7.4 Тригонометрическая и показательная формы записи комплексного числа. Действия с комплексными числами в этих формах
- •7.5 Решение задач
- •Раздел 8. Ряды.
- •8.1 Ряды. Основные определения. Признаки сходимости рядов.
- •Сходимость и расходимость рядов.
- •8.2 Необходимый признак сходимости ряда. Достаточные признаки сходимости рядов с положительными членами.
- •Достаточные признаки сходимости
- •Признак сравнения рядов
- •Методические указания по выполнению и оформлению контрольной работы
- •Контрольная работа Задание 1.
- •Задание 2.
- •Задание 3.
- •Формула разложения квадратного трёхчлена на линейные множители
1.3 Миноры и алгебраические дополнения элементов определителя.
Минором
 элемента
определителя
-го
порядка называется
определитель
элемента
определителя
-го
порядка называется
определитель
 -го порядка, получаемый из исходного
определителя вычеркиванием
-го порядка, получаемый из исходного
определителя вычеркиванием
 -ой
строки и
-ой
строки и
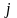 -го
столбца.
-го
столбца.
Пример
1. Найти миноры всех элементов определителя
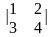 .
.
 Решение.
Решение.
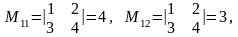

Пример
2. Найти миноры элементов
 определителя
определителя
 .
.
Решение.
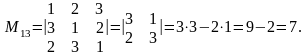
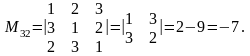
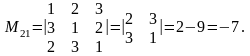
Алгебраическим
дополнением
 элемента
определителя
-го
порядка называется его
минор, взятый со знаком
элемента
определителя
-го
порядка называется его
минор, взятый со знаком
 , т.е.
, т.е.
 .
.
Из формулы видно, что перед алгебраическим дополнением берётся знак +, если сумма индексов и чётная, и знак - , если эта сумма нечётная.
Пример.
Найти алгебраические дополнения
элементов
 определителя 3-го порядка
определителя 3-го порядка
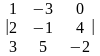 .
.
Решение.
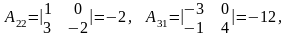

Упражнения.
Найти алгебраические дополнения всех элементов определителя:
1.
 2.
2.
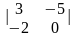
3.
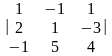 4.
4.

1.4 Вычисление определителей 3-го порядка.
Определитель 3-го порядка вычисляют двумя способами: по правилу треугольников и разложением определителя по элементам какой-либо строки (столбца)
1.4.1 Правило треугольников.
В этом случае значение определителя вычисляют как сумму шести слагаемых, каждое из которых представляет собой произведение трёх элементов определителя, выбираемых по следующему правилу: три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников берутся со знаком +,

а три произведения элементов, стоящих на побочной диагонали и в вершинах двух других треугольников берутся со знаком -- , т.е. вычисление определителя выполняется по следующей схеме:
т.е. вычисление определителя выполняется по следующей схеме:
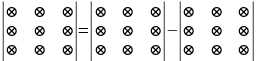
Пример.
Вычислить определитель 3-го порядка
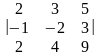 .
.
Решение.
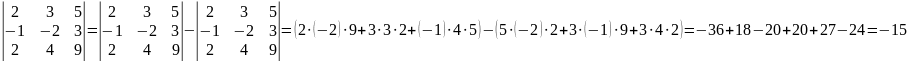
Упражнения
Вычислить определители третьего порядка по правилу треугольников:
1.
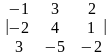 2.
2.

3.
 4.
4.
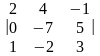
Замечание:
с помощью правила треугольников можно вычислять только определители третьего порядка.
1.4.2 Разложение определителя по элементам какой-либо строки
(столбца).
В данном случае значение определителя находят как сумму произведений элементов какой-либо строки (столбца) определителя на их алгебраические дополнения:
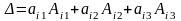 -
разложение по элементам
-ой
строки;
-
разложение по элементам
-ой
строки;
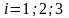 .
.
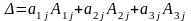 -
разложение по элементам
-ого
столбца;
-
разложение по элементам
-ого
столбца;

Пример.
Вычислить определитель 3-го порядка

Решение. Вычислим данный определитель разложением по элементам первой строки:


Замечание:
разложением по элементам какой-либо строки (столбца) вычисляют и определители высших (4-го, 5-го и т.д.) порядков, что утверждает теорема Лапласа:
определитель любого порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
 -разложение
по элементам
-ой
строки;
-разложение
по элементам
-ой
строки;

 -разложение
по элементам
-
го столбца;
-разложение
по элементам
-
го столбца;
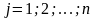 .
.
Пример.
Вычислить определитель 4-го порядка
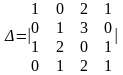 .
.
Решение. Данный определитель лучше раскладывать по элементам 1-го столбца, т.к. два элемента в нём являются нулями:

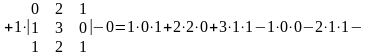

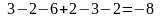 .
.
Упражнения.
№1.
Вычислить определитель третьего порядка
разложением по элементам 1-ой строки:

№2. Вычислить определитель третьего порядка разложением по элементам 3-го столбца: