Размах: быстрая и поверхностная оценка.
Размах, или интервал, занимаемый значениями данных, равен разности между самым большим и самым малым значениями. Он определяет, до какой степени отдельные значения отличаются между собой. Ниже показано вычисление размаха для небольшого набора данных, представляющих количество полученных за последнее время заказов на пять различных видов товара:
Размах набора данных (185, 246, 92, 508, 153) =
= максимальное - минимальное = 508 - 92 = 416.
Обратите внимание, что размах очень легко вычислить. Для этого нужно только просмотреть список значений, выбрать из списка самое большое и самое малое значения, а затем вычесть из большего меньшее. Раньше, до появления электронных калькуляторов и компьютеров, простота вычисления размаха была причиной того, что этот показатель часто использовался в качестве меры изменчивости. Теперь, когда вычислять стандартное отклонение стало намного проще, размах используют не так часто.
Когда важны экстремальные значения (т.е. наибольшее и наименьшее), размах может быть хорошей мерой разброса. Примером может быть необходимость описать пределы изменения значений данных. Такая характеристика может оказаться полезной для двух целей: во-первых, для описания границ изменения данных и, во-вторых, для поиска ошибок в значениях. При наличии в наборе данных очень больших (или очень малых) ошибочно записанных значений размах имеет тенденцию возрастать и сразу же становится, с позиций здравого смысла, слишком большим. Такая особенность делает размах полезным для поиска ошибок и редактирования значений данных.
С другой стороны, в силу чувствительности к предельным значениям размах оказывается не слишком полезным в качестве такой статистической меры разброса, которая характеризует набор данных в целом. Размах не отражает типичную изменчивость данных, а скорее фокусируется всего лишь на двух значениях.
Коэффициент вариации – мера относительной изменчивости.
Коэффициент
вариации, который определяется как
результат деления стандартного отклонения
на среднее значение, представляет собой
относительную
меру изменчивости и выражается в
процентах или долях среднего значения.
Такой подход особенно полезен в том
случае, когда набор данных не содержит
отрицательных значений. Формула для
вычисления коэффициента вариации (
- греческая буква «ню») для выборки имеет
следующий вид:
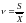
Обратите внимание на то, что стандартное отклонение стоит в числителе. Taким образом, результат деления характеризует изменчивость.
Так, например, если в среднем покупатель тратит в супермаркете $35,26, и стандартное отклонение составляет $14,08, то коэффициент вариации равен; 14,08 / 35,26 = 0,399, или 39,9%. Это означает, что обычно суммы, которые покупатель тратит при посещении супермаркета, отличаются от среднего значении примерно на 39,9% . В а6солютном выражении это типичное отличие от среднего размера затрат равно $14,08 (стандартное отклонение), что составляет 39,9% (коэффициент вариации) от среднего.
Коэффициент вариации — безразмерная величина. Это просто число, доля или процент. При вычислении коэффициента вариации размерность исчезает в результате деления стандартного отклонения на среднее значение. Коэффициент вариации полезен в тех случаях, когда важна не абсолютная величина отличий значений данных, но их относительная изменчивость.
Используя коэффициент вариации, можно сравнить вариацию объемов продаж для крупной и малой фирмы с поправкой на размер фирмы. Обычно у фирмы, оборот которой составляет сотни миллионов долларов, различия в объемах продаж также довольно велики — например, они могут достигать десятков миллионов долларов. Для другой фирмы, объем продаж которой исчисляется миллионами долларов, различия могут составлять сотни тысяч. Однако в каждом из этих двух случаев вариация составляет порядка 10% среднего значения общего объема продаж. Для большей фирмы абсолютное значение вариации окажется больше (большее стандартное отклонение), однако относительная, или учитывающая объем, величина вариации (коэффициент вариации) оказывается одинаковой для обеих фирм.
Следует также отметить, что коэффициент вариации может превысить 100% даже в том случае, если все значения положительны. Это, в частности, может быть в случае сильно скошенного распределения или при наличии значений, сильно отличающихся от среднего. Такой результат означает, что в изучаемой ситуации наблюдается очень сильная вариация по отношению к величине среднего значения.
Пример. Неопределенность доходности портфеля инвестиций.
Представьте себе, что вы вложили $10000 в 200 акций некоторой корпорации, акции которой продаются по $50 за штуку. Ваш знакомый приобрел 100 акций этой же корпорации за $5000. Вы оба ожидаете, что стоимость акций возрастет в будущем году до $60 за акцию, что соответствует ставке прибыли 20%, (60 - 50) / 50. Оба вы также считаете маркетинговую стратегию этой корпорации довольно рискованной, поскольку она характеризуется стандартным отклонением курса акций $9. Это означает, что, хоть вы и ожидаете, что стоимость одной акции составит в будущем году $60, для вас не окажется неожиданным, если она будет примерно на $9 больше или меньше этого значения.
Вы предполагаете, что объем ваших инвестиций вырастет в будущем году до $12000 ($60 * 200), со стандартным отклонением $1800 ($9 * 200). Инвестиции вашего знакомого, как ожидается, в следующем году вырастут до $6000, со стандартным отклонением $900.
Складывается впечатление, что ваш риск (стандартное отклонение в $1800) в два раза больше, чем риск вашего знакомого($900). И это действительно так, поскольку ваши инвестиции в абсолютном выражении в два раза больше. Однако оба вы делаете вложение в одни и те же ценные бумаги, а именно в акции одной й той же корпорации. Таким образом, во всех отношениях, за исключением объема инвестиций, ваша подверженность риску будет одинаковой. В относительном выражении (относительно объема первоначальных вложений) риски оказываются одинаковыми. В этом можно убедиться, вычислив коэффициент вариации (стандартное отклонение для стоимости акций в будущем году, деленное на среднее или ожидаемое значение). Коэффициент вариации в вашем случае будет равен $1800 / $12000 = 0,15, и он равен коэффициенту вариации для инвестиций вашего знакомого $900 / $6000 = 0,15. При этом и вы, и ваш знакомый будете считать, что неопределенность (или риск) составляет порядка 15% от ожидаемой в следующем году стоимости портфеля инвестиций.