Определение и формула для стандартного отклонения и дисперсии

Стандартное отклонение определяется как величина, которая вычисляется следующим образом. Обратите внимание на то, что при этом вычисляется также дисперсия (квадрат стандартного отклонения). Дисперсию иногда используют в качестве меры изменчивости в статистике, особенно когда работают непосредственно с формулами (как вы увидите в других разделах при рассмотрении дисперсионного анализа — analysis of variance, или ANOVA). Однако часто в качестве меры изменчивости лучше брать стандартное отклонение. Дисперсия не несет никакой дополнительной (по сравнению со стандартным отклонением) информации, и в то же время в практических применениях ее сложнее интерпретировать, чем стандартное отклонение. Так, например, в случае набора данных, содержащего потраченные суммы денег (измеренные в долларах), дисперсия бу­дет выражаться в “долларах в квадрате”, — это единица измерения, которую трудно себе представить; в то же время стандартное отклонение для этого набора данных будет выражено в привычных для всех долларах.

Вычисление стандартного отклонения для выборки

Для того чтобы найти стандартное отклонение для выборки, необходимо вы­полнить следующие действия.

1. Найти отклонение.

2. Возвести полученные значения в квадрат сложить и разделить сумму на n-1. Результатом будет дисперсия.

3. Извлечь из полученного значения квадратный корень. Это и будет стандартное отклонение.

В табл. 5.1.2 описанная выше процедура проиллюстрирована на примере акций компаний, выбранных выше случайным образом. В результате деления суммы возведенных в квадрат отклонений (4363,74) на n-1 получаем дисперсию 4363,74 / 3 = 1454,58. Извлекая квадратный корень, получаем стандартное отклонение 38,14. Это значение действительно является разумным описанием собственно отклонений (если не учитывать знаки и рассматривать в первую очередь величину отклонений). Стандартное отклонение можно вычислить непосредственно за один шаг в электронных таблицах Excel.

Таблица 5.1.2. Вычисление суммы квадратов отклонений, дисперсии и стандартного отклонения

Фирма	Значение	Отклонение	Квадрат откл.
Maytag Boston Scientific Catalytica Mitcham Industries	43,0 17,7 8,7 -47,4	37,5 12,2 3,2 -52,9	3706,25 148,84 10,24 2,798,41
Сумма	22,0	0,0	4363,74
Среднее	5,5

Формула для вычисления стандартного отклонения является краткой мате­матической записью описанной выше процедуры. Стандартное отклонение для выборки данных обозначается S и формулы вычисления стандартного отклонения и дисперсии имеют вид

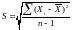
Дисперсия = S²

Выбор одного из многих различных способов расчета стандартного отклонения с помощью компьютера зависит от того, какое программное обеспечение используется: электронные таблицы, программы для работы с базами данных, компиляторы языков программирования или специальные программы для статистического анализа данных.