
- •Интегральное исчисление функций одной переменной
- •1. Первообразная. Неопределённый интеграл. Основные свойства неопределённого интеграла
- •1.1. Первообразная
- •1.2. Неопределённый интеграл, его основные свойства.
- •2. Непосредственное интегрирование. Метод подстановки. Метод интегрирования по частям.
- •2.1. Непосредственное интегрирование
- •2.2. Метод подстановки
- •2.3. Метод интегрирования по частям
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •3. Интегрирование рациональных функций
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •4. Интегрирование некоторых тригонометрических и иррациональных функций
- •4.1. Интегрирование тригонометрических функций
- •4.2. Интегрирование некоторых иррациональных функций
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •5. Понятие определённого интеграла, его геометрический смысл. Свойства определённого интеграла
- •5.1. Понятие определённого интеграла, его геометрический смысл
- •5.2. Свойства определённого интеграла
- •Аддитивность по области интегрирования.
- •Монотонность.
- •Оценка модуля интеграла.
- •Теорема о среднем.
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •6. Несобственные интегралы.
- •Примеры решения типовых задач
- •7.1.2. Площадь криволинейной трапеции в случае параметрического задания граничной кривой
- •7.2. Длина дуги кривой
- •7.2.1. Длина дуги кривой в декартовых координатах
- •7.2.2. Длина дуги кривой, заданной параметрическими уравнениями
- •7.3. Площадь поверхности вращения
- •7.3.1. Площадь поверхности вращения в декартовых координатах
- •7.3.2. Площадь поверхности вращения в случае параметрического задания кривой
- •7.4. Объём тел вращения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
Примеры решения типовых задач
Пример
1. Вычислить
определенный интеграл
 .
.
Решение.
Положим
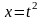
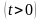 при
при

 ,
при
,
при

 .
Применим подстановку
.
Применим подстановку
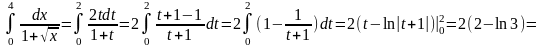
 .
.
Пример
2. Вычислить
определенный интеграл
 .
.
Решение.
Применим
метод интегрирования по частям, пусть
 .
Тогда
.
Тогда

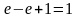 .
.
Пример
3. Вычислить
определенный интеграл
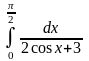 .
.
Решение. Применим универсальную тригонометрическую подстановку. Пусть
 .
Тогда
.
Тогда

 .
.
Пример
4. Оценить
интеграл
 ,
используя обобщенную теорему о среднем
9.
,
используя обобщенную теорему о среднем
9.
Решение.
Рассмотрим два случая: а)
 ;
б)
;
б)
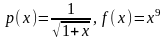 .
.
а)
 на
на
 .
Найдем наибольшее и наименьшее значения
функции
.
Найдем наибольшее и наименьшее значения
функции
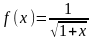 на отрезке
.
на отрезке
.
Вычислим
производную:
 ,
,
 .
.
Знаменатель
дроби обращается в нуль при
 .
Но точка
.
Но точка
 не принадлежит отрезку
,
следовательно, стационарных и критических
точек, принадлежащих отрезку
,
не существует. Найдем значения функции
не принадлежит отрезку
,
следовательно, стационарных и критических
точек, принадлежащих отрезку
,
не существует. Найдем значения функции
 на концах отрезка:
на концах отрезка:
 ,
,
 .
Таким образом,
.
Таким образом,
 ,
,
 .
.
Вычислим
интеграл
 .
.
Получаем оценку для интеграла :
 .
.
Итак,
 .
.
б)
 на
.
Аналогично пункту а) найдем наибольшее
и наименьшее значения функции
на
.
Аналогично пункту а) найдем наибольшее
и наименьшее значения функции
 на отрезке
:
на отрезке
:
 ,
следовательно,
,
следовательно,
 ,
,
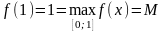 .
.
Вычислим
интеграл
 .
.
Получаем
следующую оценку
 .
.
Сравнивая две полученные оценки, делаем вывод, что наиболее точная оценка для данного интеграла была найдена в пункте а).
Задания для самостоятельной работы
8. Вычислить определенные интегралы.
|
|
|
|
|
|
|
|
|
|
9. Оценить определенные интегралы.
|
|
|
|
|
|
|
|
|
|
6. Несобственные интегралы.
Несобственные интегралы являются обобщением понятия определённого интеграла на случаи: 1) когда область интегрирования неограниченна; 2) когда подынтегральная функция неограниченна в области интегрирования.
Если
функция
непрерывна
на полупрямой
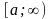 ,
то
,
то
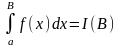 – некоторая непрерывная функция от
– некоторая непрерывная функция от
 .
Тогда, если
существует предел
.
Тогда, если
существует предел
 (6.1), то он называется несобственным
интегралом с бесконечным верхним
пределом
функции
на
и обозначается
(6.1), то он называется несобственным
интегралом с бесконечным верхним
пределом
функции
на
и обозначается
 (6.2). Таким образом
(6.2). Таким образом
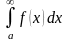 =
. (6.3)
=
. (6.3)
Н а
рис. 2 в случае неотрицательной функции
проиллюстрировано вычисление площади
фигуры, ограниченной снизу полупрямой
а
рис. 2 в случае неотрицательной функции
проиллюстрировано вычисление площади
фигуры, ограниченной снизу полупрямой
 ,
сверху графиком функции
и слева прямой
,
как предела площади криволинейной
трапеции
,
сверху графиком функции
и слева прямой
,
как предела площади криволинейной
трапеции
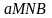 при
при
 .
.
Если предел (6.1) конечен, то интеграл (6.2) сходящийся, если бесконечен, то расходящийся. Аналогично определяется несобственный интеграл с бесконечным нижним пределом и несобственный интеграл с обоими бесконечными пределами:
 , (6.4)
, (6.4)
 , (6.5)
, (6.5)
где
 – произвольная фиксированная точка.
При этом говорят, что интеграл (6.5)
сходится, если сходится каждый из двух
несобственных интегралов в правой части
этого равенства, и расходится, если хотя
бы один из них расходится.
– произвольная фиксированная точка.
При этом говорят, что интеграл (6.5)
сходится, если сходится каждый из двух
несобственных интегралов в правой части
этого равенства, и расходится, если хотя
бы один из них расходится.
Если
сходится интеграл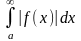 ,
то интеграл
– абсолютно сходящийся.
,
то интеграл
– абсолютно сходящийся.
Для установления сходимости интеграла (6.2) можно использовать следующие признаки сравнения.
Теорема.
Пусть всюду на полупрямой
справедливо неравенство
 .
Тогда: 1) если интеграл
.
Тогда: 1) если интеграл
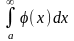 – сходится, то сходится и интеграл
,
причем
– сходится, то сходится и интеграл
,
причем
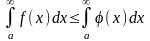 ;
2) если интеграл
расходится, то будет расходиться и
интеграл
.
;
2) если интеграл
расходится, то будет расходиться и
интеграл
.
Пусть
функция
непрерывна
во всех точках
за
исключением точки

 ,
где она
терпит бесконечный разрыв. Тогда по
определению
,
где она
терпит бесконечный разрыв. Тогда по
определению
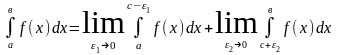 ,
где
,
где
 . (6.6)
. (6.6)
И нтеграл
(6.6) называется несобственным
интегралом
от разрывной
функции. Если оба предела, стоящие в
правой части, существуют и конечны, то
интеграл сходящийся, если хотя бы один
из них не существует или бесконечен, то
расходящийся.
нтеграл
(6.6) называется несобственным
интегралом
от разрывной
функции. Если оба предела, стоящие в
правой части, существуют и конечны, то
интеграл сходящийся, если хотя бы один
из них не существует или бесконечен, то
расходящийся.
В
случае, когда
 или
или
 (рис.3), в
правой части равенства будет только
один предел.
(рис.3), в
правой части равенства будет только
один предел.
Теорема.
Пусть всюду на отрезке
функции
,
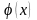 терпят бесконечный разрыв в точке
и всюду, кроме
,
выполняется
неравенство
.
Тогда: 1) если интеграл
терпят бесконечный разрыв в точке
и всюду, кроме
,
выполняется
неравенство
.
Тогда: 1) если интеграл
 – сходится, то сходится и интеграл
– сходится, то сходится и интеграл
 ;
2) если интеграл
расходится, то будет расходиться и
интеграл
.
;
2) если интеграл
расходится, то будет расходиться и
интеграл
.

 ,
,
 ;
;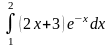 ;
; ,
,
 ;
; ;
; ,
,
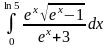 ;
;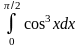 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 ;
; ,
,
 .
. ;
;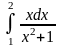 ;
;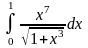 ;
; ;
;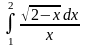 ;
; ;
; ;
; ;
;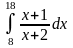 ;
;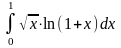 .
.