
- •Интегральное исчисление функций одной переменной
- •1. Первообразная. Неопределённый интеграл. Основные свойства неопределённого интеграла
- •1.1. Первообразная
- •1.2. Неопределённый интеграл, его основные свойства.
- •2. Непосредственное интегрирование. Метод подстановки. Метод интегрирования по частям.
- •2.1. Непосредственное интегрирование
- •2.2. Метод подстановки
- •2.3. Метод интегрирования по частям
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •3. Интегрирование рациональных функций
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •4. Интегрирование некоторых тригонометрических и иррациональных функций
- •4.1. Интегрирование тригонометрических функций
- •4.2. Интегрирование некоторых иррациональных функций
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •5. Понятие определённого интеграла, его геометрический смысл. Свойства определённого интеграла
- •5.1. Понятие определённого интеграла, его геометрический смысл
- •5.2. Свойства определённого интеграла
- •Аддитивность по области интегрирования.
- •Монотонность.
- •Оценка модуля интеграла.
- •Теорема о среднем.
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •6. Несобственные интегралы.
- •Примеры решения типовых задач
- •7.1.2. Площадь криволинейной трапеции в случае параметрического задания граничной кривой
- •7.2. Длина дуги кривой
- •7.2.1. Длина дуги кривой в декартовых координатах
- •7.2.2. Длина дуги кривой, заданной параметрическими уравнениями
- •7.3. Площадь поверхности вращения
- •7.3.1. Площадь поверхности вращения в декартовых координатах
- •7.3.2. Площадь поверхности вращения в случае параметрического задания кривой
- •7.4. Объём тел вращения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
Примеры решения типовых задач
Пример
1. Вычислить
интеграл
 .
.
Решение: Воспользуемся универсальной тригонометрической подстановкой:


Пример
2. Вычислить
интеграл
 .
.
Решение.
Используем
замену переменной
.
Тогда
 ,
,
 .
Получаем:
.
Получаем:
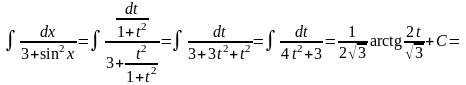
 .
.
Пример
3. Вычислить
интеграл
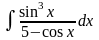 .
.
Решение.
Данная
функция нечетна относительно
.
Используем
замену переменной
.
Тогда
 и
и


Пример
4. Вычислить
интеграл
 .
.
Решение. Применив формулу (1) и табличные интегралы, получим:


Пример
5. Вычислить
интеграл
 .
.
Решение.
Воспользуемся
формулой
 .
.
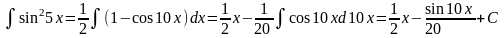 .
.
Пример
6. Вычислить
интеграл
 .
.
Решение.
Так как
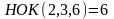 ,
то положим
,
то положим
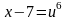 .
Тогда
.
Тогда



 и
и
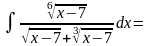

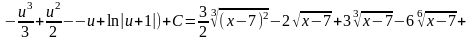

Пример
7. Вычислить
интеграл
 .
.
Решение.
Положим
 .
Тогда
.
Тогда
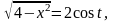
 и исходный интеграл преобразуется в
интеграл вида
и исходный интеграл преобразуется в
интеграл вида
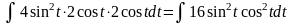 .
Интегрируя его, получим:
.
Интегрируя его, получим:

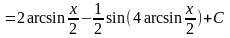 .
.
Пример
8. Вычислить
интеграл
 .
.
Решение.
Так как
 ,
то применим подстановку Эйлера
,
то применим подстановку Эйлера
 .
Отсюда
.
Отсюда
 ,
,
 ,
,
 ;
;
 ,
,
 .
.
Подставив в интеграл, получим:
 .
.
Возвращаясь к переменной , окончательно получим:
 .
.
Задания для самостоятельной работы
6. Вычислить интегралы от тригонометрических функций.
|
|
|
|
|
|
|
|
|
|
7. Вычислить интегралы от иррациональных функций.
|
|
|
|
|
|
|
|
|
|
5. Понятие определённого интеграла, его геометрический смысл. Свойства определённого интеграла
5.1. Понятие определённого интеграла, его геометрический смысл
Пусть
функция
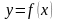 определена
на
определена
на
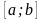 .
Разобьём
произвольным образом
точками
.
Разобьём
произвольным образом
точками
 на
частичных
отрезков длиной
на
частичных
отрезков длиной
 .
Выберем в каждом из них произвольно
точку
.
Выберем в каждом из них произвольно
точку
 и найдем значения функции в каждой из
этих точек
и найдем значения функции в каждой из
этих точек
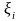 ,
то есть
,
то есть
 .
Сумма вида
.
Сумма вида
 (5.1)
(5.1)
называется n-ой интегральной суммой функции на .
Г еометрический
смысл интегральной суммы (5.1) – сумма
площадей прямоугольников с основаниями
еометрический
смысл интегральной суммы (5.1) – сумма
площадей прямоугольников с основаниями
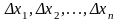 и высотами
и высотами
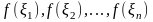 (рис.1). Обозначим через
(рис.1). Обозначим через
 длину наибольшего частичного отрезка
данного разбиения
длину наибольшего частичного отрезка
данного разбиения
 .
Найдем предел интегральной суммы
.
Найдем предел интегральной суммы
 ,
когда
,
когда
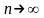 так, что
так, что
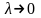 .
.
Определение.
Если существует конечный предел
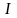 суммы (5.1),
не зависящий от способа разбиения
отрезка
на частичные
отрезки и выбора в них точек
,
то этот предел называется определённым
интегралом
от функции
по отрезку
и обозначается:
суммы (5.1),
не зависящий от способа разбиения
отрезка
на частичные
отрезки и выбора в них точек
,
то этот предел называется определённым
интегралом
от функции
по отрезку
и обозначается:
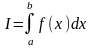 .
.
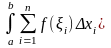 ,
,
– подынтегральная
функция,
– подынтегральное
выражение,
– отрезок
интегрирования,
и
 – нижний и
верхний пределы интегрирования,
– переменная
интегрирования.
– нижний и
верхний пределы интегрирования,
– переменная
интегрирования.
Теорема. Если функция непрерывна на , то она интегрируема на , т.е. предел интегральной суммы (5.1) существует.
Если
 ,
то геометрически определённый интеграл
выражает площадь фигуры, ограниченной
графиком функции
,
осью
,
то геометрически определённый интеграл
выражает площадь фигуры, ограниченной
графиком функции
,
осью
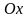 и прямыми
и прямыми
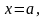
 .
Эта фигура называется криволинейной
трапецией.
.
Эта фигура называется криволинейной
трапецией.
В
общем случае, когда функция
на отрезке
принимает
значения разных знаков, определённый
интеграл выражает разность площадей
криволинейных трапеций, расположенных
над осью
и под ней,
т.к.
 расположенной под осью
,
принимает отрицательное значение.
расположенной под осью
,
принимает отрицательное значение.

 ;
;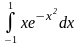 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;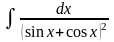 .
. ;
;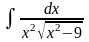 ;
; ;
;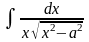 :
: ;
;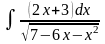 ;
;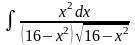 ;
; ;
; ;
; .
.