Задания для самостоятельной работы

 4. Вычислить интеграл от дроби, содержащий в знаменателе квадратный трехчлен.

;	;
;	;
;	;
;	;
;	.

 5. Вычислить интегралы от рациональных функций.

;	;
;	;
;	;
;	;
;	.

4. Интегрирование некоторых тригонометрических и иррациональных функций

В этом параграфе для интегралов от некоторых классов тригонометрических и иррациональных выражений будут даны рационализирующие подстановки, то есть замены переменной, приводящие исходный интеграл к интегралу от рациональной дроби. Здесь через 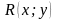будем обозначать рациональные выражения относительно и , то есть выражения, полученные путем применения конечного числа раз к аргументам и операций сложения, вычитания, умножения, деления и композиции функций.

4.1. Интегрирование тригонометрических функций

I. Интегралы вида приводятся к интегралам от рациональной функции новой переменной с помощью универсальной тригонометрической подстановки . В этом случае .

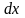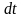Подставляя в подынтегральное выражение вместо их выражения через , получим интеграл от рациональной дроби:

.

В случае, когда имеет место тождество

для приведения подынтегральной функции к рациональному виду можно применять упрощённую подстановку . При этом .

Если 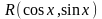– нечетная функция относительно 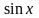, т.е. , то интеграл рационализируется подстановкой .

Если – нечетная функция относительно , т.е. , то интеграл рационализируется подстановкой .

II. Для отыскания интегралов вида

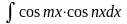используют следующие формулы:

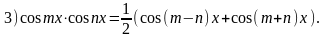
При нахождении интегралов вида возможны следующие случаи:

1) хотя бы одно из чисел или 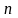– нечетное, например , тогда

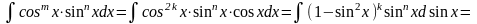
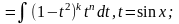
2) оба числа или – четные, тогда рекомендуется использовать следующие формулы, позволяющие понизить степень тригонометрических функций: ,

4.2. Интегрирование некоторых иррациональных функций

Не для всякой иррациональной функции можно найти первообразную в виде элементарной функции. Рассмотрим интегралы от некоторых иррациональных функций, которые с помощью определённых подстановок приводятся к интегралам от рациональных функций новой переменной.

I. Интеграл вида , где – постоянные, приводятся к интегралу от рациональной функции новой переменной с помощью подстановки , где наименьшее общее кратное (НОК) знаменателей дробей 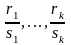, т.е. .

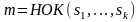II. Интегралы вида

тригонометрическими подстановками соответственно сводятся к уже рассмотренным интегралам вида .

К рассмотренным интегралам могут быть преобразованы интегралы 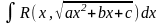, если из квадратного трёхчлена выделить полный квадрат суммы и сделать линейную замену переменной.

Если в трехчлене , то интеграл рационализируется подстановкой Эйлера .

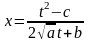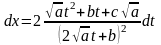Возведя обе части равенства в квадрат, получаем , , , .Таким образом,

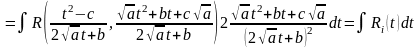, где 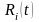– рациональная функция от .

Если же в трехчлене 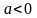, а , то для рационализации интеграла можно применить другую подстановку Эйлера: .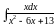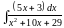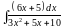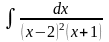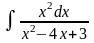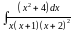