Задания для самостоятельной работы
1. Вычислить интегралы.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
и)
|
к)
|
;
;
;
;
;
;
;
;
;
. 2. Вычислить интегралы с помощью метода замены переменной.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;
;
;
;
;
;
;
;
;
.
3. Вычислить интеграл методом интегрирования по частям.
|
|
|
|
|
|
|
|
|
|
,
;
,
;
,
;
,
;
,
;
,
;
,
;
,
;
,
;
,
.
3. Интегрирование рациональных функций
Рациональными
функциями
называются функции вида
,
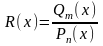где
– многочлены степени
соответственно. Приведём необходимые
в дальнейшем сведения из алгебры о
рациональных функциях.
Число
называется
корнем или нулём многочлена
,
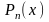если
Теорема
Безу. Многочлен
делится без остатка на
тогда и только тогда, когда число а
является
корнем данного многочлена.
Таким
образом,
Корень а
называется
k-кратным,
если
,
где
.
Рациональная дробь называется правильной,
если степень числителя меньше степени
знаменателя. В противном случае называется
неправильной. Всякую неправильную
рациональную дробь можно, деля числитель
на знаменатель, представить в виде суммы
многочлена, называемого целой частью
дроби, и правильной рациональной дроби.
Например:
.
Будем
рассматривать правильные рациональные
дроби с действительными коэффициентами
многочленов в числителе и знаменателе.
Среди них назовём простейшими дроби
вида:
,
,
.
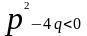Теорема
(о разложении правильной дроби в сумму
простейших дробей). Всякую рациональную
правильную дробь со знаменателем
представимым в виде произведения можно
разложить в виде суммы простейших
рациональных дробей типа 1) – 2). В данном
разложении каждому корню
кратности
многочлена
соответствует сумма k
дробей вида
,
где
– действительные числа, называемые
неопределёнными коэффициентами.
Примеры решения типовых задач
Рассмотрим два наиболее простых способа нахождения неопределённых коэффициентов на одном конкретном примере.
Пример
1. Вычислить
интеграл
.
Решение. I метод – метод неопределённых коэффициентов.
Разложим
знаменатель на линейные и квадратичные
множители с действительными коэффициентами:
и запишем разложение данной дроби на
простейшие с неопределёнными
коэффициентами:
.
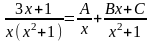Приведя к общему знаменателю правую
часть, получим равенство числителей:
.
Приравниваем коэффициенты при одинаковых степенях в правой и левой частях этого равенства.
При
.
При
.
При
.
Тогда
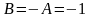и
.
Далее находим неопределённый интеграл:
II метод – метод частных значений.
Придадим аргументу столько различных значений, сколько имеется неопределённых коэффициентов, используя в первую очередь корни знаменателя.
,
,
.
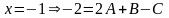Тогда получим систему независимых
уравнений, из которой имеем:
.
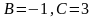Пример
2. Вычислить
интеграл
.
Решение.
Представим дробь в виде суммы простейших
дробей с неопределёнными коэффициентами:
.
Приведя дроби в обеих частях к общему
знаменателю, получим:
.
Найдём неопределённые коэффициенты
методом частных значений, придадим
аргументу
последовательно значения –1, 1, 0. Получим
систему:
,
откуда
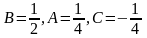и
.
Таким образом:
.
Пример
3. Вычислить
интеграл
.
Решение. Выделим целую часть дроби:
.
Разложим знаменатель дроби на множители с действительными коэффициентами:
.
Умножая это равенство на общий знаменатель,
получим:
.
Приравняем коэффициенты при одинаковых
степенях
слева и
справа.
При
.
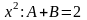При
.
При
.
Тогда
и
.
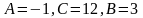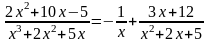Итак, вычислим неопределённый интеграл:
.
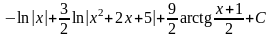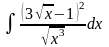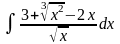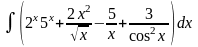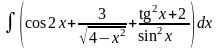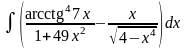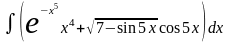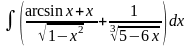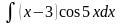
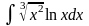
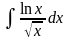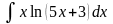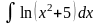
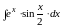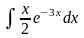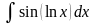