Интегральное исчисление функций одной переменной
1. Первообразная. Неопределённый интеграл. Основные свойства неопределённого интеграла
1.1. Первообразная
Одной
из основных задач дифференциального
исчисления является отыскание производной
заданной функции. Разнообразные вопросы
математического анализа и его
многочисленные приложения в геометрии,
механике, физике и технике приводят к
обратной задаче: по данной функции
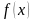найти
такую функцию
,
что
.
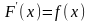Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления.
Функция
называется
первообразной
для функции
на некотором
промежутке
,
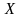если она дифференцируема на этом
промежутке и для всех
выполняется равенство
.
Например,
первообразной функции
является функция
,
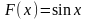так как
.
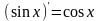Аналогично для функции
первообразной
является
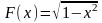т.к.
.
Задача
отыскания по данной функции
её первообразной решается неоднозначно.
Например,
То есть, первообразными будут любые
функции
,
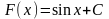где
– постоянная.
Теорема
1.1. Если
первообразная
для функции
на некотором
промежутке
,
то любая другая первообразная для
на том же промежутке может представлена
в ви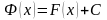де
,
где
–
произвольная постоянная.
Доказательство.
Пусть
–
любая другая первообразная для функции
на
некотором промежутке Х,
т.е.
.
Рассмотрим
где
.
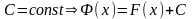1.2. Неопределённый интеграл, его основные свойства.
Определение.
Совокупность всех первообразных для
функции
на промежутке
называется неопределённым
интегралом от
функции
и обозначается
,
где
– знак интеграла,
– подынтегральная функция,
– подынтегральное выражение.
Восстановление функции по её производной, или, что то же самое, отыскание неопределённого интеграла по данной подынтегральной функции, называется интегрированием этой функции. Интегрирование представляет собой операцию обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Например,
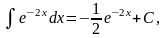т.к.
.
Аналогично
т.к.
.
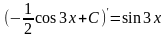Из определения неопределенного интеграла непосредственно вытекают следующие свойства:
Производная неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению, т.е.
.
Действительно,
;
Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
.Постоянный множитель можно вынести из под знака интеграла, т.е. если
,
,
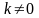то
.
Действительно,
пусть
–
первообразная
,
тогда
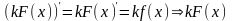– первообразная для
.
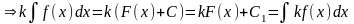Неопределённый интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций, т.е.
.
Действительно,
пусть
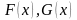– первообразные для функций
,
,
тогда функция
– первообразная для функции
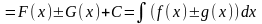
2. Непосредственное интегрирование. Метод подстановки. Метод интегрирования по частям.
2.1. Непосредственное интегрирование
Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределённых интегралов называется непосредственным интегрированием. То есть непосредственное интегрирование – это сведение данного интеграла к табличному путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла. Ниже приведена таблица интегралов от основных элементарных функций.
Таблица основных интегралов:
1)
2)
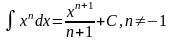
3)
4)
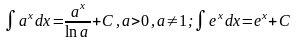
5)
6)
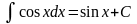
7)
8)
9)
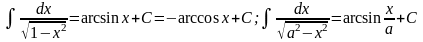
10)
11)
12)
.