1 Барьерная емкость электронно-дырочного перехода

1.1 Барьерная емкость как проявление токов смещения

Барьерная емкость p-n-перехода проявляется при приложении к р-n-переходу изменяющегося во времени напряжения. При этом через p-n-переход проходит ток. Та доля тока, которая не связана с движением носителей заряда через р-n-переход, и определяет барьерную емкость. Барьерная емкость связана с прохождением токов смещения.

Для одномерного плоского р-n-перехода ток (плотность тока) смещения, одинаковый во всех его сечениях,

(3.14)

где S — площадь р-n-перехода.

Значение тока смещения можно связать с изменением объемного заряда. Для этого выделим мысленно в p-n-переходе объем в виде цилиндра (или призмы), образующие которого параллельны оси x — направлению электрического поля (рис. 3.11).

Рис.3.11 .К выводу выражения для

барьерной емкости p-n-перехода

Одно основание цилиндра пусть лежит за пределами р-n-перехода, а другое — внутри его. Тогда, согласно теореме Остроградского — Гаусса, можно определить поток вектора электрической индукции через поверхность, ограничивающую выделенный объем. Этот поток проходит только через одно основание цилиндра, так как боковые его поверхности параллельны электрическому полю, а второе основание лежит в области, где поле отсутствует. Тогда

(3.15)

где Q — заряд ионизированных примесей.

Ток смещения можно записать теперь таким образом:

(3.16)

Сравнив последнее выражение с обычным выражением для тока через емкость, т.е. с

получаем, что в качестве барьерной емкости следует взять величину

(3.17)

Абсолютное значение этого отношения взято потому, что объемный заряд в р-n-переходе может быть положительным и отрицательным, а правило знаков для напряжения выбрано произвольно.

Таким образом, барьерная емкость связана с током смещения (как и обычная емкость).

1.2 Общее соотношение для барьерной емкости электронно-дырочного перехода

Исходя из определения барьерной емкости (3.17), можно получить общую формулу для барьерной емкости плоского p-n-перехода. Объемный заряд ионизированных примесей в цилиндре, выделенном в р-n-переходе,

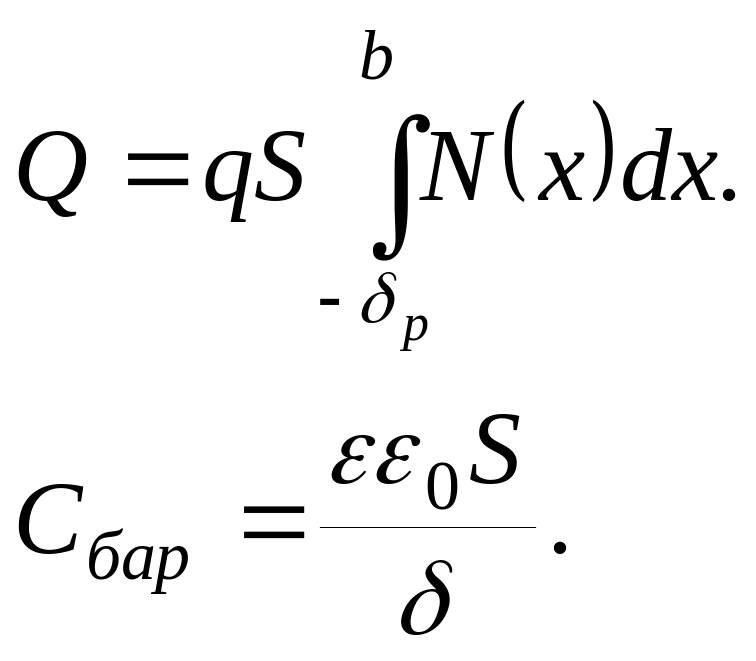(3.18)

где б –расстояние между слоями.

Таким образом, барьерная емкость плоского одномерного р-n-перехода может быть рассчитана по формуле плоского конденсатора.

Такой результат не является очевидным, так как распределение зарядов в плоском конденсаторе и в электронно-дырочном переходе не одинаково. Причина совпадения формул — в характере изменения заряда р-n-перехода: при изменении напряжения на р-n-переходе заряд изменяется потому, что сдвигаются границы р-n-перехода.

Заряды, обусловливающие барьерную емкость, сосредоточены в двух тонких слоях, расположенных на расстоянии в одиночестве от другого (рис. 3.11), что очень напоминает поверхностные заряды на металлических обкладках конденсатора.

1.3 Частные соотношения для барьерной емкости различных электронно-дырочных переходов

С помощью выражения (3.18) можно определить барьерную емкость на основе результатов расчета толщины р-n-перехода. Поэтому для резкого p-n-перехода,

(3.19)

Для резкого несимметричного р-n-перехода

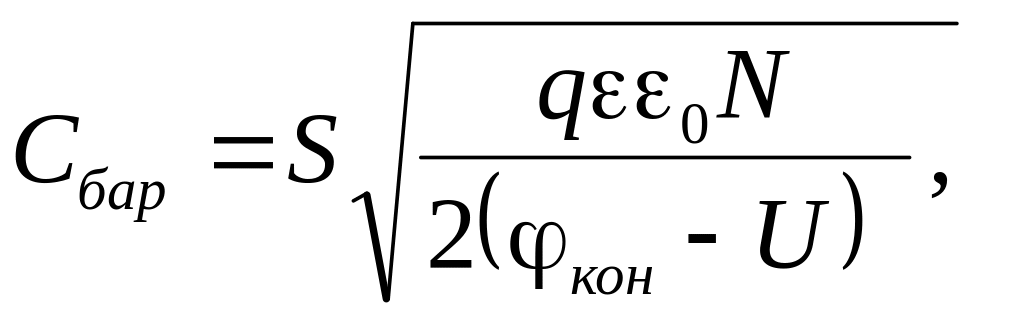(3.20)

где N — концентрация примесей в слаболегированной области.

Для плавного р-n-перехода с линейным распределением концентрации примесей

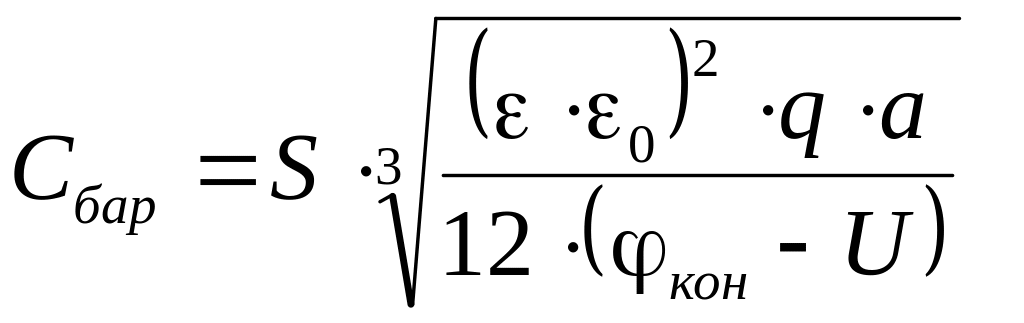, (3.21)

где а – градиент концентрации заряда