1.Прямая и точка плоскости. Условие принадлежности.

Прямая принадлежит плоскости, если две точки этой прямой

принадлежат данной плоскости. Точка принадлежит

плоскости, если она принадлежит прямой

принадлежащей данной плоскости. Точка ортогональной

проекцией точки на пл. проекции называют основание

перпендикуляра опущенного из данной точки к плск.

Проекции. Прямые соединяющие проекции точек

и перпендикулярные оси проекции называются линиями

проекционной связи

2. Положение прямых в пространстве. Графический

признак прямых частного положения.

Прямые частного положения:

Прямая не перпендикулярная и не параллельная оси

проекции называется прямой общего положения.

Прямая параллельная или перпендикулярная называется

прямой частного положения . прямые параллельные

оси проекции называются линии уровня. Прямые

перпендикулярные оси проекции называются проецирующими.

3. Частные положения прямых в пространстве, графические

признаки их изображения на эпюре.

К прямым уровня относятся: 1) горизонталь h- прямая, || плоскости П1;

2) фронталь f- прямая, || плоскости П2;

3) профильная прямая АВ- прямая, || плоскости П3

К проецирующим прямым относятся: 1) горизонтально проецирующая прямая CD- прямая, перп. Плоскости П1;

2) фронтально проецирующая пряма EF- прямая, перп. Плоскости П2;

3)профильно проецирующая прямая АВ- прямая, перп. Плоскости П3.

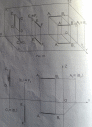
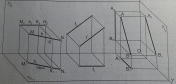
4. Определение истинной величины отрезка прямой

методом прямоугольного треугольника.

Натуральная величина прямой АБ равна гипотенузе

Треугольника, катетом которого является проекция отрезка

АБ на пл. проекции, а вторым катетом разность координат

до линии уровня.

5. Способы определения натуральной величины

отрезка. Привести примеры.

1 Определить НВ отрезка методом прямоугольного треугольника.

2 определить НВ отрезка методом замены плоскостей проекции:

Для этого прямую общего положения превращаем в линию

уровня при помощи введения новой плс проекции , и после

проецируем данную прямую на новую плс проекции.

3 способ вращения : доворачиваем проекцию прямой до линии

уровня, после при помощи линий проекционной связи находим

НВ отрезка на смежной плс проекции.

6. Графический признак параллельных, пересекающихся

и скрещивающихся прямых.

Параллельные прямые: если одноименные проекции прямых

параллельны во всех плоскостях проекции, то эти прямые

параллельны в пространстве.

Пересекающиеся прямые : прямые пересекаются в пространстве

если одноименные проекции этих прямых пересекаются , и

точки пересечения лежат на одной линии связи.

Скрещивающиеся прямые: одноименные проекции прямых

пересекаются но точки пересечения не лежат на одной линии

связи. У прямых параллельных плоскости проекции, одна

из проекций параллельна оси проекции.

7. Графические признаки прямых частного положения

относительно плоскости проекций. Главный признак прямой частного положения: они расположены

в пространстве параллельно одной из плс проекции.

Проецирующая прямая-прямая перпендикулярная плс проекции,

на эпюре одноименная проекция обращается в точку другая

перпендикулярна оси проекции.