Закон розподілу ймовірностей (приклад 4.1)

Подія	Дохідність, %	Ймовірність
Підйом	12	0,33
Без зміни	9	0,33
Спад	6	0,33

На практиці ймовірності того, що доходність за акціями буде дорівнювати 12, 9, або 6% невеликі. Однак можливо, що при даному обсязі та якості доступної інформації такий розподіл видався аналітикам найбільш правдоподібним.

У загальному випадку можна побудувати багато подібних сценаріїв розвитку подій, визначивши, наприклад, межі зміни попиту від повної відсутності до невиданого буму і задавши відповідні ймовірності. Однак й отримана в результаті таблиця розподілів може бути настільки великою, що стане непридатною або незручною для практичного застосування.

Тому для зручності проведення аналізу розподіли випадкових дискретних величин апроксимують неперервними розподілами, що дозволяють використовувати порівняно прості методи розрахунків навіть при необмеженій кількості сценаріїв. Для задання таких розподілів використовується функція F(x), що називається функцією розподілу випадкової величини.

Функцією F(x) розподілу ймовірностей випадкової величини Е називається ймовірність того, що вона набуде значення, яке не перевищує число х:

(4.5)

Якщо функція розподілу F(x) неперервна і її можна диференціювати, то її похідна називається щільністю розподілу ймовірностей. Тоді функцію розподілу ймовірностей можна визначити як:

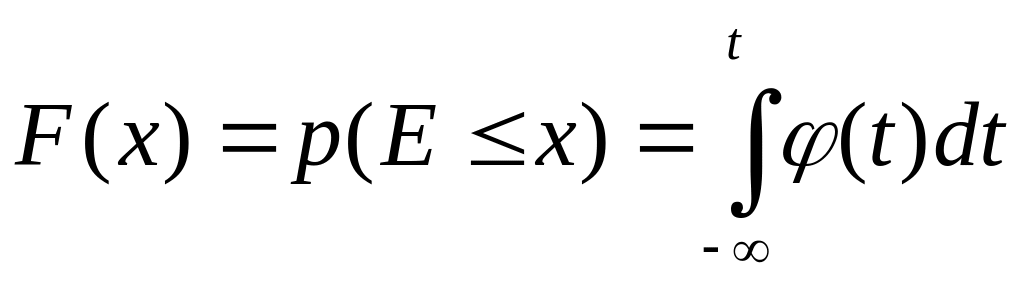(4.6)

де змінюється на відрізку [0; 1]; - значення функції щільності ймовірностей випадкової величини Е.

Функція дає повну інформацію про закон розподілу випадкової величини. Таким чином, знаючи функцію (закон) розподілу або щільність розподілу ймовірностей випадкової величини, можна робити висновки про ступінь достовірності здійснення подій, що її породжують.

Однак для вирішення багатьох практично важливих задач часто буває достатньо знати значення лише декількох характеристик (параметрів) випадкової величини, що дають менш повніше, але більш наочне уявлення про її розподіл. Найважливіші із них: середнє (очікуване) значення, дисперсія і стандартне (середнє квадратичне) відхилення.

Середнє (очікуване) значення випадкової величини

Концепція середнього широко використовується практично у всіх сферах людської діяльності. Середній вік, середні обсяги споживання, середня заробітна плата, середня доходність – все це далеко не повний перелік показників, які щоденно зустрічаються у засобах масової інформації. Концепція середнього не лише корисна, але й інтуїтивно зрозуміла. У фінансовому моделюванні, говорячи про середні величини, часто використовують термін «очікуване значення».

Середнім, або очікуваним, значенням (математичним очікуванням)

дискретної випадкової величини Е називається сума добутку її значень на їх ймовірності.

(4.7)

Виділяють такі важливі властивості цього показника:

1. постійний множник С можна винести за знак математичного очікування:

; (4.8)

2. математичне очікування суми двох випадкових величин дорівнює сумі їх математичних очікувань:

; (4.9)

3. математичне очікування постійної величини С дорівнює цій величині:

; (4.10)

4. математичне очікування добутку незалежних випадкових величин дорівнює добутку їх математичних очікувань:

(4.11)

Визначимо математичне очікування (тобто середнє, або очікуване, значення доходності) для прикладу 4.1:

.

Таким чином, середня (очікувана) доходність за акціями дорівнює 9%. Неважко помітити, що у випадку рівної ймовірності настання кожної із подій (тобто, при ) математичне очікування випадкової величини обчислюється як арифметичне середнє:

(4.12)

Математичне очікування (середнє, або очікуване, значення) – одна із найважливіших характеристик випадкової величини, оскільки служить центром розподілу її ймовірностей¹. Сенс цієї характеристики для прикладу, що розглядається, полягає у тому, що вона представляє собою найбільш правдоподібну міру річної доходності за акціями фірми «Н».

Однак дана характеристика, взята сама по собі, не дозволяє виміряти ступінь ризику операції, що здійснюється. Розглянемо наступний приклад.

Приклад 4.2

Розглядається можливість придбання акцій двох фірм «А» і «В». Отримані експертні оцінки передбачуваних значень доходності за акціями та їх ймовірності представлені у табл. 4.2.

Таблиця 4.2

Значення доходності за акціями та їх ймовірності (приклад 4.2)

Прогноз	Ймовірність	Доходність, %
		Фірма «А»	Фірма «В»
Песимістичний	0,3	-70	10
Ймовірний	0,4	15	15
Оптимістичний	0,3	100	20

Як випливає із табл. 4.2., середня доходність по акціях обох фірми однакова і складає 15%. Однак величини отриманих доходів в найбільш сприятливому випадку, як і величини можливих збитків в найбільш несприятливому, будуть суттєво відрізнятися. На рис. 4.1 та 4.2 наведені графіки функцій щільності розподілу ймовірностей для прикладу, що розглядається.

Рис. 4.1. Щільність розподілу ймовірностей (акції «А»)

Рис. 4.2. Щільність розподілу ймовірностей (акції «В»)

Неважко пімітити, що ймовірнісний розподіл очікуваного доходу по акціях фірми «В» згрупований навколо середнього значення (15%) щільніше. Відповідно, ймовірність того, що реальна доходність по цих акціях буде нижчою за середню, значно менша, ніж по акціях фірми «А», і можна сказати, що акції фірми «В» менш ризикові.

У загальному випадку, чим менший діапазон ймовірного розподілу очікуваної доходності по відношенню до її середньої величини, тим менший ризик, пов'язаний із даною операцією.

Кількісне обгрунтування останнього твердження може бути отримане визначенням двох інших характеристик розподілу випадкової величини – дисперсії та стандартного відхилення.

Дисперсія і стандартне відхилення випадкової величини

Дисперсія і стандартне відхилення служать характеристиками розкиду (варіації) випадкової величини від її центру розподілу (середнього значення М(Е)). Необхідність і корисність застосування цих порказників добре ілюструє старий анекдот про математика, який свято вірив у значимість середніх величин і потонув у річці, чередня глибина якої не перевищувала половини його росту.

Дисперсією називається сума квадратів відхилень випадкової величини від її середнього значення, зважених на відповідні ймовірності:

(4.13)

Відзначимо наступні властивості цього показника:

1. дисперсія постійної величини дорівнює 0;

2. для будь-якої невипадкової постійної С:

, (4.14)

. (4.15)

Розрахуємо дисперсії доходності по акціях фірм «А» та «В». Вони відповідно складуть:

.

Наведені розрахунки дають кількісне підтвердження результатам графічного аналізу. Розкид доходності відносно середнього значення, а відповідно і ризик, по акціях фірми «В» значно менший, ніж по акціях фірми «А».

Незважаючи на те, що дисперсія може служити мірою ризику фінансових операцій, її застосування не завжди зручне. Як слідує із (4.13), розмірність дисперсії дорівнює квадрату одиниці вимірювання випадкової величини.

На практиці результати аналізу більш очевидні, якщо показник розкиду випадкової величини виражений у тих самих одиницях вимірювання, що й сама випадкова величина. Для цих цілей в якості міри розкиду випадкової величини зручно використовувати інший показник – стандартне (середнє квадратичне) відхилення, що розраховується за формулою:

(4.16)

Звідси випливає, що величина представляє собою середньозважене відхилення випадкової величини від її математичного очікування, при цьому в якості ваг беруться відповідні ймовірності. Будучи виражене у тих самих одиницях, стандартне відхилення показує, наскільки значення випадкової величини можуть відрізнятися від її середнього.

Відповідно, чим менше стандартне відхилення, тим вужчий діапазон ймовірнісного розподілу і тим нижчий ризик, пов'язаний із даною операцією.

Із (4.16) також слідує, що:

(4.17)

Розрахуємо стандартне відхилення для нашого прикладу:

; .

Знаючи закон розподілу ймовірностей та його основні параметри, можна робити висновки про ступінь ризику операції, що здійснюється. Однак слід завжди пам’ятати про те, що ці висновки будуть також носити ймовірнісний характер.