
Чудесенко 15 вариант (1-22 -11)
.pdf
Задачник Чудесенко, теория вероятностей, 15 вариант
1) Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит N 9 ; б) произведение числа очков не превосходит N 9 ; в) произведение числа очков делится на N 9 .
Решение:
C61 6 способами можно выбрать цифру на одной игральной кости;
C61 6 способами можно выбрать цифру на другой игральной кости.
Таким образом, общее число исходов (возможных комбинаций цифр на двух игральных костях): C61 C61 6 6 36
а) Найдем вероятность того, что сумма очков превосходит N 9 . Подсчитаем количество благоприятствующих исходов:
10очков: (4,6),(6,4),(5,5)
11очков: (5,6),(6,5)
12очков: (6,6)
Всего: 6 благоприятствующих исходов.
По классическому определению вероятности:
q 366 16 – вероятность того, что сумма очков превзойдет 9. По теореме сложения вероятностей противоположных событий:
p1 1 q 1 16 56 – вероятность того, что сумма очков не превзойдет 9
б) Подсчитаем количество благоприятствующих исходов: 1 очко: (1,1)
2 очка: (1,2),(2,1)
3 очка: (1,3),(3,1)
4очка: (1,4),(4,1),(2,2)
5очков: (1,5),(5,1)
6очков: (1,6),(6,1),(2,3),(3,2)
8очков: (2,4),(4,2)
9очков: (3,3)
Всего: 17 благоприятствующих исходов.
По классическому определению вероятности:
p2 1736 – вероятность того, что произведение очков не превзойдет 9.
в) Подсчитаем количество благоприятствующих исходов: 9 очков: (3,3)
18 очков: (3,6),(6,3)
27 очков: –
36 очков: (6,6)
Всего: 4 благоприятствующих исхода.
По классическому определению вероятности:
p3 364 19 – вероятность того, что произведение очков делится 9.
Ответ: а) p1 56 , б) p2 1736 , в) p3 19
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
1 |
Задачник Чудесенко, теория вероятностей, 15 вариант |
|
|
|
|
|
|||||||||||||||||
2) Имеются изделия четырех сортов |
n1 2 , n2 3 , |
n3 4 , n4 |
2 . Для контроля |
|||||||||||||||||||
наудачу берутся |
m |
|
изделий. Определить |
вероятность |
того, что |
среди них |
m1 1 |
|||||||||||||||
первосортное, m2 |
2 , m3 |
2 и m4 1 второго, 3-го и четвертого сорта соответственно. |
||||||||||||||||||||
Решение: Всего: n 2 3 4 2 11 изделий. Размер выборки: m 1 2 2 1 6 |
||||||||||||||||||||||
C6 |
|
|
11! |
7 8 9 10 11 462 способами можно выбрать 6 изделий из 11. |
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||
11 |
|
|
|
|
5! 6! |
|
|
|
120 |
|
|
|
|
|
|
|
|
|||||
C21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 способами можно выбрать изделие 1-го сорта; |
|
|
|
|||||||||||||||||||
C2 |
3 способами можно выбрать два изделия 2-го сорта; |
|
|
|||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C42 |
6 способом можно выбрать два изделия 3-го сорта; |
|
|
|||||||||||||||||||
C21 2 способами можно выбрать изделие 4-го сорта. |
|
|
|
|||||||||||||||||||
C21 C32 |
C42 |
C21 |
2 3 6 2 72 |
– способами можно выбрать искомую комбинацию |
||||||||||||||||||
изделий. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По классическому определению вероятностей: |
|
|
|
|||||||||||||||||||
p |
|
C1 |
C2 |
C2 |
C1 |
|
72 |
|
12 |
– искомая вероятность. |
|
|
||||||||||
|
|
2 |
3 |
|
4 |
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
462 |
77 |
|
|
|||||||||
|
|
|
|
|
|
|
|
C6 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: p 12 |
0,1558 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3) Среди |
n 8 |
лотерейных билетов |
k 4 выигрышных. Наудачу взяли |
m 5 |
||||||||||||||||||
билетов. Определить вероятность того, что среди них l 2 выигрышных. |
|
|||||||||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
C5 |
|
|
8! |
6 7 8 56 способами можно выбрать 5 билетов из 8-ми. |
|
|||||||||||||||||
|
|
|
||||||||||||||||||||
8 |
|
|
|
3! 5! |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|||||
C42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6 способами можно выбрать два выигрышных билета из 4-х; |
|
|||||||||||||||||||||
C43 4 способами можно выбрать три безвыигрышных билета из 4-х. |
|
|||||||||||||||||||||
C42 C43 |
6 4 24 способами можно выбрать искомую комбинацию билетов. |
|
||||||||||||||||||||
По классическому определению вероятности: |
|
|
|
|||||||||||||||||||
p |
|
C2 |
C3 |
|
24 |
|
3 |
– искомая вероятность. |
|
|
|
|||||||||||
|
|
4 |
4 |
56 |
7 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
C5 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: p 3 |
0,4286 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4) В лифт k 8 - этажного дома сели n 3 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что: а) все вышли на разных этажах; б) по крайне мере двое сошли на одном этаже.
Решение:
C71 7 способами может выйти каждый пассажир из лифта.
C71 C71 C71 7 7 7 342 способами могут выйти три пассажира из лифта а) Рассмотрим событие: A – пассажиры выйдут из лифта на разных этажах.
A3 |
5 6 7 210 способами можно разместить пассажиров по трем разным |
7 |
|
этажам (с учетом перестановок пассажиров).
По классическому определению вероятностей:
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
2 |
Задачник Чудесенко, теория вероятностей, 15 вариант
P(A) |
A3 |
C71 |
|
210 |
|
35 |
– вероятность того, что все пассажиры выйдут на |
C71 C71 |
342 |
57 |
|||||
|
7 |
|
|
|
|
|
|
разных этажах.
б) Рассмотрим событие: A – по крайне мере двое сошли на одном этаже. События A и A являются противоположными, поэтому P(A) P(A) 1, следовательно:
P(A) 1 P(A) 1 5735 5722 – искомая вероятность. Ответ: а) P(A) 5735 0,61, б) P(B) 5722 0,39 .
5) В отрезке единичной длины наудачу появляется точка. Определить вероятность того, что расстояние от точки до концов отрезка превосходит величину k1 81 .
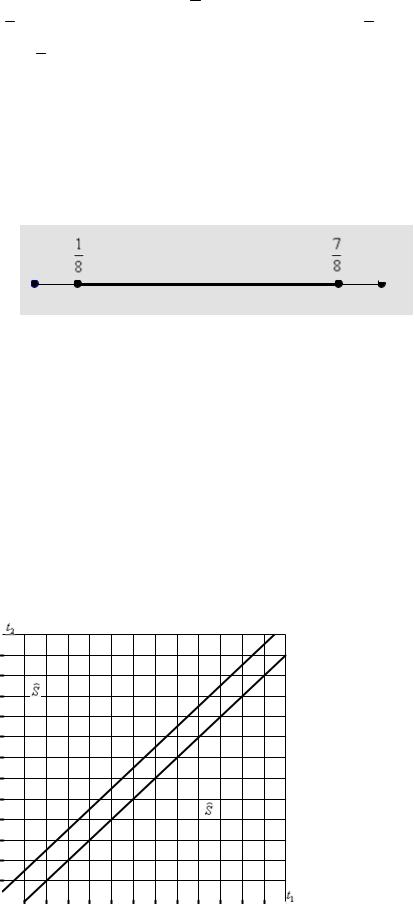
Решение: Выполним чертеж:
X
0 |
1 |
Общему числу исходов соответствует длина единичного отрезка l 1. Благоприятствующему числу исходов соответствует длина l 78 18 34 . По геометрическому определению вероятностей:
p ll 34 – вероятность того, что расстояние от точки до концов отрезка
превосходит величину 18 .
Ответ: p 34
6) Моменты начала двух событий наудачу распределены в промежутке времени от T1 1200 до T2 1330 . Одно из событий длится 10 мин., другое – t 5 мин. Определить вероятность того, что: а) события «перекрываются» во времени; б) «не перекрываются».
130 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Промежуток времени: |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t T2 T1 130 . Выполним чертеж. |
|||||
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общему |
|
числу |
исходов |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соответствует |
|
|
площадь |
||
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S 130 130 16900 |
|
||||
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Благоприятствующему числу |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
исходов соответствует площадь |
||||||
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 125 |
120 120 15012,5 . |
||||
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
2 |
2 |
|||
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По |
геометрическому |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определению вероятности: |
|
|||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
|
|
|
|
|
|||
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
3 |

Задачник Чудесенко, теория вероятностей, 15 вариант
p SS 1501216900,5 13521201 – вероятность того, что события «не перекрываются» во времени. а) Найдем вероятность противоположного события:
p 1 13521201 1352151 – вероятность того, что события «перекрываются» во времени. Ответ: а) p 1352151 0,1117 , б) p 13521201 0,8883 .
7) В круге радиуса R 11 наудачу появляется точка. Определить вероятность того, что она попадет в одну из двух непересекающихся фигур, площади которых равны
S1 2,2 и S2 3,5
Решение: Вычислим площадь круга:
Sкр R2 112 121
Суммарная площадь непересекающихся фигур:
S S1 S2 2,2 3,5 5,7 .
По геометрическому определению вероятности:
p |
S |
|
5,7 |
0,015 – искомая вероятность. |
|
Sкр |
121 |
||||
|
|
|
Ответ: p 5,7 0,015 121
8) В двух партиях k1 76% , k2 42% доброкачественных изделий соответственно.
Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное?
Решение: Из условия следует, что:
p1 0,76 , p2 0,42 – вероятности того, что изделие из соответствующей партии
является доброкачественным. Тогда, вероятности того, что изделие из соответствующей партии является бракованным:
q1 1 p1 1 0,76 0,24;
q2 1 p2 1 0,42 0,58. а) Рассмотрим события:
A – хотя бы одно изделие является бракованным; A – оба изделия доброкачественны.
События A и A являются противоположными, поэтому: P(A) P(A) 1.
По теореме умножения независимых событий: P(A) p1 p2 0,76 0,42 0,3192 . Таким образом:
P(A) 1 P(A) 1 0,3192 0,6808 – искомая вероятность.
б) Рассмотрим событие:
B – оба изделия бракованны.
По теореме умножения независимых событий:
P(B) q1q2 0,24 0,58 0,1392 – искомая вероятность.
в) Рассмотрим событие:
C – одно изделие бракованное и одно доброкачественное.
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
4 |
Задачник Чудесенко, теория вероятностей, 15 вариант
По теоремам сложения несовместных и умножения независимых событий:
P(C) p1q2 |
q1 p2 0,76 0,58 0,24 0,42 0,4408 0,1008 0,5416 |
– |
искомая |
вероятность. |
|
|
|
Ответ: а) P(A) 0,6808 , б) P(B) 0,1392 , с) P(C) 0,5416 . |
|
|
|
9) Вероятность того, что цель поражена при одном выстреле первым стрелком |
|||
p1 0,76 , вторым |
p2 0,39 . Первый сделал n1 2 выстрела, второй n2 |
3 |
выстрелов. |
Определить вероятность того, что цель не поражена.
Решение: найдем вероятность промаха для соответствующих стрелков: q1 1 p1 1 0,76 0,24;
q2 1 p2 1 0,39 0,61.
По теореме умножения независимых событий:
p q q q |
q |
q |
2 |
(0,24)2 |
(0,61)3 |
0,013074 – вероятность того, что цель не |
||
1 |
1 |
2 |
2 |
|
|
|
|
|
поражена.
Ответ: p 0,013074
10) Два игрока A и B поочередно бросают монету. Выигравшим считается тот, у кого раньше выпадет герб. Первый бросок делает игрок A , второй – B , третий – A и т.д. Найти вероятность того, что выиграл A не позднее k 10 броска.
Решение: p 12 – вероятность выпадения герба;
q 12 – вероятность выпадения цифры.
Рассмотрим несовместные исходы, соответствующие выигрышу игрока A : 1) p1 p 12 ;
3) p3 qqp 12 12 12 18 ;
|
|
|
|
|
|
|
|
|
1 5 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5) |
p5 |
qqqqp |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 7 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7) |
p7 |
qqqqqqp |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
128 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
9) |
p9 |
qqqqqqqqp |
1 |
9 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
512 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По теореме сложения несовместных событий: |
|
|
|
|
|||||||||||||||||||||||||||||||||
p p p |
p |
|
p |
7 |
p |
1 |
1 |
1 |
|
|
|
1 |
|
|
1 |
|
341 – вероятность того, что |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
1 |
|
3 |
|
5 |
|
|
|
|
9 |
|
|
|
2 |
8 |
32 |
|
|
128 |
|
512 |
|
512 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
игрок A выиграет не позднее 10 броска. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Найдем вероятность выигрыша каждого игрока при сколь угодно длительной игре. |
|||||||||||||||||||||||||||||||||||||
Вероятность выигрыша игрока A : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
P(A) |
1 |
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
... |
1 |
|
|
|
|
|
|
|
|
|
|
|
... |
(*) |
||||||||||||
2 |
8 |
32 |
128 |
|
4 |
42 |
43 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
5 |

Задачник Чудесенко, теория вероятностей, 15 вариант
Используем формулу для вычисления суммы членов бесконечно убывающей
геометрической прогрессии: |
|
|
||||||
Sn |
x1 |
|
|
|
|
|
|
|
1 g |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
(*) |
1 |
1 |
1 |
4 |
|
2 |
– искомая вероятность. |
|
1 1 |
|
|||||||
|
2 |
2 |
3 |
|
3 |
|
||
|
|
4 |
|
|
|
|
|
|
Вероятность выигрыша игрока B : |
||||||||
P(B) 1 P(A) 1 |
2 |
|
1 |
|||||
|
|
|
|
|
|
3 |
|
3 |
Ответ: p 512341 0,6660156 , P(A) 23 , P(B) 13
12) Из 1000 ламп соответствующим партиям принадлежат n1 640 , n2 80 , n3 280 ламп. В первой партии 6%, во второй 5%, в третьей 4% бракованных ламп. Наудачу выбирается одна лампа. Определить вероятность того, что лампа – бракованная.
Решение: Всего: 1000 ламп. Тогда:
p1 1000640 0,64 , p2 100080 0,08 , p3 1000280 0,28 – вероятность выбора лампы из соответствующей партии.
Из условия следует, что:
p1 0,06 , p2 0,05 , p3 0,04 – вероятности того, что лампа соответствующей
партии является бракованной.
По формуле полной вероятности:
p p1 p1 p2 p2 p3 p3 0,64 0,06 0,08 0,05 0,28 0,04
0,0384 0,004 0,0112 0,0536
–вероятность того, что наудачу извлеченная лампа будет бракованной.
Ответ: p 0,0536
13) В первой урне N1 6 белых и M1 4 черных шара, во второй N2 3 белых и M2 3 черных. Из первой во вторую урну переложено K 4 шара, затем из второй урны извлечен один шар. Найти вероятность того, что выбранный из второй урны шар – белый.
Решение: Всего: 6 + 4 = 10 шаров в первой урне.
C4 |
|
10! |
|
7 8 9 |
10 210 способами можно выбрать 4 шара из первой урны. |
|
|||||
10 |
|
6! 4! |
24 |
|
|
|
|
|
|||
Рассмотрим следующие несовместные исходы:
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
6 |
Задачник Чудесенко, теория вероятностей, 15 вариант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
Извлечено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Во 2-ой урне стало |
Вероятность |
||||
исхода |
из первой урны |
|
Соответствующая |
|
извлечения |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
белого шара |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
вероятность |
|
|
||||||||||||||||||
|
белых |
черных |
|
|
белых |
черных |
|
из второй |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
урны |
1 |
4 |
0 |
4 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
3 |
7 |
|
||
|
|
|
|
C6 |
C4 |
|
|
|
15 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|||||||||||||
|
|
|
|
C104 |
210 |
|
14 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
3 |
1 |
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
4 |
6 |
|
||
|
|
|
|
C6 |
C4 |
|
|
|
20 4 |
|
|
8 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
10 |
|
||||||||||||||||
|
|
|
|
C104 |
210 |
|
21 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
5 |
|
||
|
|
|
|
C6 |
C4 |
|
|
15 6 |
|
3 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
10 |
|
|||||||||||||||
|
|
|
|
C104 |
|
210 |
|
7 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
1 |
3 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
4 |
|
||
|
|
|
|
C6 |
C4 |
|
|
|
6 4 |
|
|
|
4 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
||||||||||||
|
|
|
|
C104 |
|
210 |
|
35 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5 |
0 |
4 |
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
7 |
3 |
|
||
|
|
|
|
C6 |
C4 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
||||||||
|
|
|
|
C104 |
|
210 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
По теоремам сложения несовместных и умножения зависимых событий:
|
p |
|
1 |
|
7 |
|
|
|
8 |
|
6 |
|
3 |
|
5 |
|
|
4 |
|
|
4 |
|
1 |
|
3 |
|
27 – вероятность того, что из второй |
|||||||||||||||||||||
|
14 |
|
|
|
|
|
7 |
|
35 |
|
|
210 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
10 |
|
|
21 |
10 |
|
|
|
|
10 |
|
|
|
10 |
|
|
10 |
|
50 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
урны будет извлечен белый шар. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Ответ: p 27 |
0,54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
14) В альбоме |
k 6 |
чистых и l 8 гашеных марок. Из них наудачу извлекают |
|||||||||||||||||||||||||||||||||||||||||||||
|
m 3 марки (среди которых могут быть и чистые и гашеные), которые подвергаются |
|||||||||||||||||||||||||||||||||||||||||||||||
|
спецгашению и возвращаются в альбом. После этого вновь наудачу извлекается n 2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
марки. Определить вероятность, что все n марок чистые. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
Решение: Всего: 6 + 8 = 14 марок в альбоме. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
C3 |
|
|
14! |
|
12 13 14 364 способами можно выбрать 3 марки из альбома; |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
14 |
|
|
11! 3! |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
C2 |
|
|
|
14! |
|
|
13 14 |
91 способами можно выбрать 2 марки из альбома; |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
14 |
|
|
12! 2! |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Рассмотрим следующие несовместные исходы: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
№ |
Извлечены марки |
|
|
Соответствующая |
|
Стало марок |
|
Вероятность того, что |
||||||||||||||||||||||||||||||||||||||||
исхода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
все извлеченные марки |
|
|||||||||||||||||||||||||
чистые |
|
гашеные |
|
|
|
|
вероятность |
|
|
|
|
|
чистых |
гашеных |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чистые |
|
1 |
3 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
4 5 6 |
|
|
|
20 |
|
3 |
|
|
|
11 |
2 |
|
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C6 C8 |
|
|
|
|
|
|
|
|
|
|
C3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C3 |
|
|
|
|
|
|
6 364 |
|
|
364 |
|
|
|
|
|
|
|
C2 |
|
91 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
||
2 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
15 8 |
|
|
120 |
|
|
4 |
|
|
|
10 |
2 |
|
|
6 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C6 C8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
C4 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C3 |
|
|
|
|
|
364 |
|
|
364 |
|
|
|
|
|
|
|
|
C2 |
|
91 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
||
3 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
6 28 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
9 |
2 |
|
10 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C6 C8 |
|
|
|
|
|
168 |
|
|
|
|
|
|
C5 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C3 |
|
|
|
|
|
364 |
|
|
364 |
|
|
|
|
|
|
|
|
C2 |
|
91 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
||
4 |
0 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
|
56 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
8 |
2 |
|
15 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C6 C8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C6 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C3 |
|
|
|
|
|
364 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
91 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
||
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
7 |

Задачник Чудесенко, теория вероятностей, 15 вариант |
|
|
|
|
|
|
|
|
|
|
|||||||||||
По теоремам сложения несовместных и умножения зависимых событий: |
|
|
|||||||||||||||||||
p |
20 |
|
3 |
|
|
120 |
6 |
|
168 |
10 |
56 |
15 |
3300 |
|
825 |
|
– вероятность |
того, что |
|||
|
|
|
91 |
364 |
|
||||||||||||||||
364 |
91 |
|
364 |
364 |
91 |
91 |
33124 |
8281 |
|
|
|
|
|||||||||
обе извлеченные марки будут чистыми. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ответ: p |
|
825 |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
8281 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
15) В магазин поступают однотипные изделия с трех заводов: m1 70 , |
m2 20 , |
||||||||||||||||||||
m3 10 . Среди |
изделий |
соответствующих |
заводов |
n1 70% , |
n2 80% , |
|
n3 90% |
||||||||||||||
первосортных. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено 3-м заводом.
Решение: Всего: 100 изделий. Тогда: |
|
|
|
|
|
|||||||||
p |
70 |
|
0,7 , p |
2 |
|
20 |
0,2 , |
p |
|
10 |
0,1 – |
вероятности |
того, что изделие |
|
|
|
|
|
|||||||||||
1 |
100 |
|
|
100 |
|
3 |
100 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
выпущено соответствующим заводом. |
|
|
|
|
|
|
||||||||
Из условия следует, что: |
|
|
|
|
|
|
||||||||
p1 0,7 , |
p2 0,8 , |
p3 0,9 – |
вероятности того, |
что изделие |
соответствующего |
|||||||||
завода является первосортным.
По формуле полной вероятности:
p p1 p1 p2 p2 p3 p3 0,7 0,7 0,2 0,8 0,1 0,9
0,49 0,16 0,09 0,74
–вероятность того, что купленное изделие оказалось первосортным. По формуле Байеса:
p p2pp2 0,740,09 749 0,1216 – вероятность того, что купленное первосортное изделие выпущено 3-м заводом.
Ответ: p 749 0,1216
16) Монета бросается до тех пор, пока герб не выпадет n 2 раза. Определить вероятность того, что цифра выпадает m 3 раза.
Решение: p 1 |
, q 1 |
– вероятности выпадения герба и цифры соответственно. |
||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
Используем формулу Бернулли: |
|
|||||||||
Pk Ck pk ql k , в данной задаче: |
|
|||||||||
l |
l |
|
|
|
|
|
|
|
|
|
1 |
1 1 |
q |
3 |
4 |
|
1 1 |
3 |
1 |
– вероятность того, что в первых четырех |
|
P4 |
C4 p |
|
|
|
|
|
4 |
|||
|
|
|
|
|
|
2 |
2 |
|
|
|
испытаниях выпадет один герб и 3 цифры.
p5 12 – вероятность того, что в 5-ом испытании выпадет второй герб. По теореме умножения независимых событий:
p P41 p5 14 12 18 – искомая вероятность.
Ответ: p 18 0,125
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
8 |
Задачник Чудесенко, теория вероятностей, 15 вариант
17) Вероятность выигрыша в лотерею на 1 билет равна p 0,5 . Куплено n 11
билетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность.
Решение: Найдем наивероятнейшее количество выигравших билетов (математическое ожидание):
M np 11 0,5 5,5 6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Найдем соответствующую вероятность, используем формулу Бернулли: |
|
|||||||||||||||||||
Pm |
C m pm qn m , в данном случае: |
|
|
|
|
|
|
|
||||||||||||
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P6 |
C6 |
(0,5)6 (0,5)5 |
|
11! |
(0,5)11 |
7 8 9 10 11 (0,5)11 |
0,225586 |
– |
искомая |
|||||||||||
|
||||||||||||||||||||
11 |
11 |
|
|
|
|
|
5! 6! |
|
|
|
|
120 |
|
|
|
|
|
|||
вероятность. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: M 6 , P6 0,225586 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
18) |
На |
|
каждый |
|
лотерейный |
билет с |
вероятностью |
p1 0,09 |
может |
выпасть |
||||||||||
крупный |
выигрыш, с |
вероятностью |
p2 |
0,21 |
– мелкий |
выигрыш и |
с вероятностью |
|||||||||||||
p3 0,7 билет |
может |
оказаться |
|
без |
выигрыша. Куплено |
n 14 билетов. Определить |
||||||||||||||
вероятность получения n1 1 крупного выигрыша и n2 |
3 мелких. |
|
|
|||||||||||||||||
Решение: Используем полиномиальное распределение вероятности. |
|
|||||||||||||||||||
P m ,m ,...,m |
|
|
n! |
|
|
pm1 pm2 |
...pmk |
|
|
|
|
|
|
|||||||
|
m !m !...m |
|
|
|
|
|
|
|
||||||||||||
n |
1 |
2 |
|
k |
|
! 1 |
2 |
k |
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
2 |
|
k |
|
|
|
|
|
|
|
|
|
|
||
В данном случае: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
P 1,3,10 |
14! |
(0,09)1 (0,21)3 |
(0,7)10 0,0943 |
– вероятность того, что из 14 |
||||||||||||||||
|
||||||||||||||||||||
14 |
|
|
1!3!10! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
купленных билетов на 1 будет получен крупный выигрыш и на 3 – мелкие выигрыши.
Ответ: P14 1,3,10 0,0943
19) Вероятность «сбоя» в работе телефонной станции при каждом вызове равна p 0,02 . Поступило n 300 вызовов. Определить вероятность m 8 «сбоев».
Решение: Используем формулу Пуассона:
Pm m e , в данной задаче: m!
np 300 0,02 6 – среднее количество сбоев;
m 8 .
Таким образом:
P 68 |
e 6 |
0,1033 – вероятность того, что будет ровно 8 сбоев. |
|
8 |
8! |
|
|
|
|
|
|
Ответ: P8 0,1033
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
9 |

Задачник Чудесенко, теория вероятностей, 15 вариант |
|
20) Вероятность наступления некоторого события в каждом из |
n 100 |
независимых испытаний равна p 0,6 . Определить вероятность того, что |
число m |
наступления событий удовлетворяет неравенству m 65 . |
|
Решение: Используем интегральную теорему Лапласа:
Pn (m1 m m2 ) (k2 ) (k1 ) , где (x) – функция Лапласа; В данной задаче:
n 100 – всего испытаний;
p 0,6 – вероятность наступления события в каждом испытании;
q 1 p 1 0,6 0,4 – вероятность ненаступления события в каждом испытании. По соответствующим формулам найдем k1 и k2 :
k2 |
m2 |
np |
|
100 100 |
0,6 |
|
40 |
|
|
|
8,16 ; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
npq |
|
100 0,6 |
0,4 |
24 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
k |
m1 |
np |
65 100 0,6 |
|
|
5 |
|
|
|
1,02 . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
npq |
|
|
100 0,6 0,4 |
|
|
24 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Таким образом:
P100 (65 m 100) (8,16) (1,02) 0,5000 0,3461 0,1539 – вероятность того, что в 100 независимых испытаниях событие наступит не менее 65 раз.
Ответ: P100 (m 65) 0,1539 |
|
2, x ;3 , |
случайной величины X . |
21) Дана плотность распределения f (x) |
|
0, x ;3 . |
|
Найти параметр , математическое ожидание M (X ) , дисперсию D(X ) , функцию распределения случайной величины X , вероятность выполнения неравенства 1 X 3 .
Решение: Функция плотности распределения вероятности обладает свойством
f (x)dx 1. В данном случае:
3
2 dx 1 2 x 3 1 2(3 ) 1 3 0,5 2,5
Таким образом, функция плотности распределения:
2, x 2,5;3 , f (x) 0, x 2,5;3 .
Вычислим математическое ожидание:
|
|
|
|
3 |
|
|
|
|
|
1 |
x2 |
|
|
9 6,25 2,75 |
|
|
|
|
|
|
|||||||
M (X ) xf (x)dx 2 xdx 2 |
|
32,5 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2,5 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дисперсию вычислим по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(X ) x2 f (x)dx (M (X ))2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В данном случае: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 2 |
|
|
11 |
2 |
2 |
x |
3 |
|
|
3 |
|
121 |
|
2 |
|
|
125 |
|
121 |
|
91 |
|
121 |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
D(X ) 2 x |
dx |
|
|
|
|
|
|
5 2 |
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2,5 |
|
|
4 |
|
3 |
|
|
|
|
|
|
16 |
|
3 |
|
|
8 |
|
16 |
|
12 |
|
16 |
|
48 |
||
Другие решения можно найти здесь: http://mathprofi.ru/skachat_primery_po_vysshei_matematike.html |
10 |
