
- •1. Источники и составные части теории автоматического управления
- •30-60-Е гг:
- •2. Классификация систем автоматического управления
- •3.Собственные и вынужденные колебания в системах.
- •4. Частотные характеристики систем автоматического управления
- •5. Передаточные функции. Связь между входом и выходом системы в частотной области.
- •6. Передаточные функции основных видов соединения систем.
- •7. Передаточные функции по управлению и по возмущению
- •8. Статические и астатические системы
- •9. Типовые воздействия
- •10. Связь между входным и выходным процессами во временной области
- •11. Амплитудно и фазочастотные характеристики (годограф Найквиста)
- •12.Логарифмические характеристики (диграмма Боде):
- •13. Типовые звенья: идеальное интегрирующее звено
- •15. Колебательное звено.
- •16 Дифференцирующее звено первого порядка
- •17. Дифференцирующее звено второго порядка.
- •18 Звено чистого запаздывания
- •19. Устойчивость: Условие устойчивости линейной системы
- •20. Принцип аргумента
- •21. Критерий Рауса-Гурвица
- •22. Критерий Найквиста
- •23.Запасы устойчивости: по амплитуде и по фазе
- •24. Прямые показатели качества систем регулирования и управления
- •25. Интегральные показатели качества
- •26. Определение дисперсии ошибки системы при случайном воздействии
- •27. Определение взаимной корреляционной функции входа и выхода по автокорреляционной функции входного сигнала
- •28. Определение импульсной переходной функции статистическим методом
- •29. Определение импульсной переходной функции по входу и выходу (детерминированных процессов)
- •30. Описание дискретных систем уравнениями в конечных разностях
- •31. Z-передаточная функция дискретной системы.
- •32 Условие устойчивости линейной дискретной системы. Критерий Рауса-Гурвица.
21. Критерий Рауса-Гурвица
![]() характеристический
полином n-го
порядка
характеристический
полином n-го
порядка
Определитель Гурвица для системы n-го порядка
Имеет размер n x n
Заполняется по следующему правилу
На главной диагонали
записываются коэффициенты
![]() в порядке возрастания
в порядке возрастания
Вниз в сторону убывания коэффициенты располагаются вверх по столбцам в порядке возрастания
Матрица

Там где индекс отрицательный он не пишется, а заменяется 0
С индексами больше чем n нулями
Чтобы система была
устойчивой необходимо и достаточно
чтобы при
![]() все главные миноры тоже были >0
все главные миноры тоже были >0![]()
22. Критерий Найквиста
Это частотный критерий суждения об устойчивости и о многом другом происходит по частотным характеристикам: по годографу Найквиста. Он занимался задачей проектирования усилителя.
По критерию Найквиста суждения об устойчивости замкнутой системы происходит по годографу разомкнутой:
1) Судят об устойчивости замкнутой с-п.
2) Что сделать за счёт замкнутой, чтоб она была устойчива.
Пусть передаточная
функция разомкнутой системы
![]()
Передаточная функция замкнутой цепи при единичной обратной связи.
![]()

![]()
Рассмотрим частотную хар-ку:
![]() -- отношение хар-го
полинома замкнутой системы к хар-му
полиному разомкнутой системы.
-- отношение хар-го
полинома замкнутой системы к хар-му
полиному разомкнутой системы.
![]()
![]() (2)
(2)
Приращение аргумента хар-го полинома разомкнутой системы равна …. (см. выше).
Если разомкнутая система устойчива, то приращение аргумента равно:
![]() ,
где n-порядок
характерного уравнения.
,
где n-порядок
характерного уравнения.
Порядок хар-ого уравнения замкнутой и разомкнутой системы совпадает.
Для того, чтоб замкнутая система была устойчивой, все корни хар-ого уравнения должны лежать в левой полуплоскости, т.е.
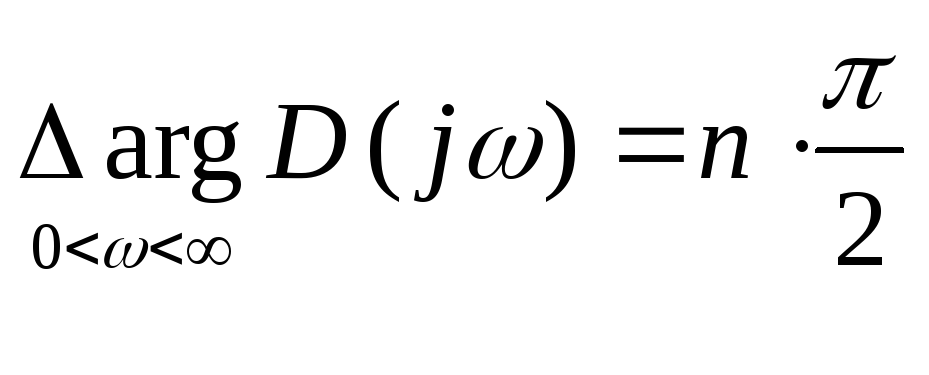
Для того, чтобы система устойчивая в разомкнутом состоянии была устойчива в разомкнутом состоянии, необходимо и достаточно, чтобы:
![]()

![]()
Годограф
![]() и годограф
и годограф![]() совпадают
если сместить ось ординат на единицу
влево. При изменении
совпадают
если сместить ось ординат на единицу
влево. При изменении![]() от 0 до
от 0 до![]() годограф
годограф![]() описывает кривую и ее приращение (угол
поворота) должен равняться 0 (с нуля
начался в ноль пришел)
описывает кривую и ее приращение (угол
поворота) должен равняться 0 (с нуля
начался в ноль пришел)
Вектор
![]() не должен охватывать (.)
не должен охватывать (.)
(-1; jo)
(*)
Необходимо и
достаточно, чтобы вектор
![]() не охватывал точку (-1;jo).
не охватывал точку (-1;jo).
Пусть разомкнутая система не устойчива и имеет n корней в правой полуплоскости, тогда приращением аргумента хар-го полинома разомкнутой системы равно:

Если замкнутая система устойчива, то приращение аргумента замкнутой системы равно:

В соответствии с уравнением (2), для того, чтобы система не устойчивая в разомкнутом состоянии и имеющая n корней в правой полуплоскости, была устойчива в замкнутом состоянии необходимо и достаточно, чтобы:

или (что тоже самое)
годограф
![]() должен охватить начало координатk/2
раз.
должен охватить начало координатk/2
раз.
Д ля
того чтобы система устойчивая в
разомкнутом состоянии, сk
корнями в правой полуплоскости, была
устойчива в разомкнутом состоянии
необходимо и достаточно, чтобы частотная
хар-ка
ля
того чтобы система устойчивая в
разомкнутом состоянии, сk
корнями в правой полуплоскости, была
устойчива в разомкнутом состоянии
необходимо и достаточно, чтобы частотная
хар-ка
![]() охватила точку (-1;jo)
k/2
раз в положительном направлении; k
– число корней хар-го уравнения в правой
полуплоскости.
охватила точку (-1;jo)
k/2
раз в положительном направлении; k
– число корней хар-го уравнения в правой
полуплоскости.
![]()
 -- передаточная
функция по ошибке.
-- передаточная
функция по ошибке.
![]() --
коэффициент статической ошибки
--
коэффициент статической ошибки
![]()
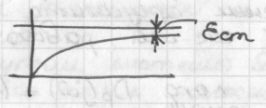
С истемы
в которых увеличение коэффициента
усиления не приводит к захвату -1,
называются абсолютно устойчивыми
(системы 2-й степени).
истемы
в которых увеличение коэффициента
усиления не приводит к захвату -1,
называются абсолютно устойчивыми
(системы 2-й степени).

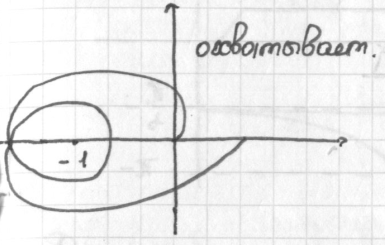
Путем введения
звеньев можно перейти к устойчивой
системе (рис. см. выше). В статических
системах при
![]() хар-ка стремится к номинальному числу.
хар-ка стремится к номинальному числу.
В астатических начинается от
астатических начинается от![]() стр. в 0.
стр. в 0.
.

Не охватывает, астатизм первого порядка Охватывает, астатизм 2-го порядка.
