
- •1. Источники и составные части теории автоматического управления
- •30-60-Е гг:
- •2. Классификация систем автоматического управления
- •3.Собственные и вынужденные колебания в системах.
- •4. Частотные характеристики систем автоматического управления
- •5. Передаточные функции. Связь между входом и выходом системы в частотной области.
- •6. Передаточные функции основных видов соединения систем.
- •7. Передаточные функции по управлению и по возмущению
- •8. Статические и астатические системы
- •9. Типовые воздействия
- •10. Связь между входным и выходным процессами во временной области
- •11. Амплитудно и фазочастотные характеристики (годограф Найквиста)
- •12.Логарифмические характеристики (диграмма Боде):
- •13. Типовые звенья: идеальное интегрирующее звено
- •15. Колебательное звено.
- •16 Дифференцирующее звено первого порядка
- •17. Дифференцирующее звено второго порядка.
- •18 Звено чистого запаздывания
- •19. Устойчивость: Условие устойчивости линейной системы
- •20. Принцип аргумента
- •21. Критерий Рауса-Гурвица
- •22. Критерий Найквиста
- •23.Запасы устойчивости: по амплитуде и по фазе
- •24. Прямые показатели качества систем регулирования и управления
- •25. Интегральные показатели качества
- •26. Определение дисперсии ошибки системы при случайном воздействии
- •27. Определение взаимной корреляционной функции входа и выхода по автокорреляционной функции входного сигнала
- •28. Определение импульсной переходной функции статистическим методом
- •29. Определение импульсной переходной функции по входу и выходу (детерминированных процессов)
- •30. Описание дискретных систем уравнениями в конечных разностях
- •31. Z-передаточная функция дискретной системы.
- •32 Условие устойчивости линейной дискретной системы. Критерий Рауса-Гурвица.
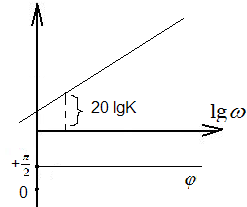
12.Логарифмические характеристики (диграмма Боде):

![]() -
эти две характеристики построены в
логарифмическом масштабе частот, наз.
логарифмическ. амплитудно- частотной
и фазочастотной характеристиками
(диаграмма Боде).
-
эти две характеристики построены в
логарифмическом масштабе частот, наз.
логарифмическ. амплитудно- частотной
и фазочастотной характеристиками
(диаграмма Боде).

Изменение частоты в 2 раза называется изменением частоты на октаву, а в 10 раз – на декаду: lg(2w)-lg(w) = lg2
lg(10w)-lg(w)=lg10=1
lg10 – децибел
Логарифмические характеристики послед. соед. складываются.
![]()

Во многих случаях логарифмические амплитудные хар-ки могут быть заменены асимптотическими, т.е. отрезками прямых.
13. Типовые звенья: идеальное интегрирующее звено
![]()
 ;
;

![]()
![]()
Если среди n
корней есть
![]() действительных
корней и
действительных
корней и![]() -комплексно
сопряженных,
-комплексно
сопряженных,
причем
![]()
![]() +
+![]() , тогда
, тогда
![]() можно представить в виде:
можно представить в виде:


![]()
w(S)=
n=![]()
Таким образом передаточную функцию можно представить как последовательное соединение некоторых типовых звеньев (b звеньев):
1.Усилительное звено: w(S)=K
2.Апериодическое
звено: w(S)=![]()
3. Колебательное
звено: w(S)=![]()
4.Чисто интегрирующее
звено: w(S)=![]()
5. Чисто дифференцирующее звено:w(S)=K*S
6. Дифференцирующее
звено 1-го порядка: w(S)=![]()
7.Дифференцирующее
звено 2-го порядка: w(S)=![]()
8. Звеночистого
запаздывания : w(S)=![]()
![]()
Рассмотрим усилительное звено (идеальное интегрирующее звено): w(S)=K
K(t)=k![]() ,
h(t)=
,
h(t)=![]()
![]() ,
w(iw)=k=k
,
w(iw)=k=k![]()

14.Апериодическое звено:
![]()
Дифференциальное уравнение, которое описывает это звено.
![]() (1)
(1)
Частотные характеристики:
![]()
![]() (2)
(2)
 (3)
(3)



![]()
Низкочастотные
![]() ;
при такомw,
что
;
при такомw,
что
![]()
Высокочастотные
![]() ;
при
;
при![]()
![]()
Ур-ие- прямая с наклоном -20дб/дек.
![]() --
точка
сопряжения
--
точка
сопряжения
20lgk=20lgk-20lgTw
=> lgTw
= 0 =>
![]()

|
w |
|
|
|
|
|
|
|
-0,1 |
-3 |
-1 |
-1 |
-0,1 |
![]()

15. Колебательное звено.
Описывается Д.У. 2-го порядка
![]()
![]()
![]()
![]() ,
корни характеристического уравнения.
,
корни характеристического уравнения.
Корни могут быть ggg
Уравнение с действительными коэффициентами
В случае, когда
 ,
то 2 корня действительны. Послед.
Соединение 2-х апериодических звена с
одинаковой константой времени.
,
то 2 корня действительны. Послед.
Соединение 2-х апериодических звена с
одинаковой константой времени.При единичном ступенчатом воздействии. Если внешнее воздействие положить = 1, то единичная переходная
 функция как решение уравнения 2-го
порядка.
функция как решение уравнения 2-го
порядка.


Чем меньше
![]() (коэффициент демфирования) (демфер
предназначен на сглаживание колебаний),
тем колебательность больше.
(коэффициент демфирования) (демфер
предназначен на сглаживание колебаний),
тем колебательность больше.
Т-const времени и время в долях постоянной времени. Длительность процесса зависит от Т.
Логарифмические хар-ки:

have 2 асимптоты: высоко- и
низкочастотная
частота
сопряжения:
![]()
фазовая
хар-ка
max ошибка – 3db и max достигается на частоте сопряжения.
При 0,38≤![]() ≤0,7
ошибка в пределах ±3db.
при 0,7 – ниже
≤0,7
ошибка в пределах ±3db.
при 0,7 – ниже
![]() при 0,38 – выше
при 0,38 – выше![]()
При
![]() ошибка – -6db,
при 0,7<
ошибка – -6db,
при 0,7<![]() ≤1
ошибка от – 6 до 3db(графики
сглаживаются)
≤1
ошибка от – 6 до 3db(графики
сглаживаются)
При малом
![]() поправки сущ-ют в частоте сопряжения.
Частота резонанса (
поправки сущ-ют в частоте сопряжения.
Частота резонанса (![]() зашел в резонанс). Система чрезвычайно
колебательна и управлять ей сложно.
зашел в резонанс). Система чрезвычайно
колебательна и управлять ей сложно.![]() показывает связи с колебательной
системой. Чем выше
показывает связи с колебательной
системой. Чем выше![]() ,
тем резче переход.
,
тем резче переход.
Идеально диф-щее.
![]()
16 Дифференцирующее звено первого порядка
Передаточная функция:
![]()

