7. Передаточные функции по управлению и по возмущению

-передаточная функция по управлению.

-передаточная функция по возмущению.

Уравнение (*) коротко записывают так

1.D(p)=B(p)Z+C(p)f

B(p)- полином m-ой степени от р.

С(р)- полином к-ой степени от р.

к-символ дифференцирования.

При такой записи по управлению

При возмущении

2) A(p)Z=M(P)

3) =x-y

(2)- Исключение координат из системы алгебраических уравнений.

-передаточная функция в замкнутой системе по управлению.

-передаточная функция в замкнутой системе по возмущению.

-Передаточная ф-ция по ошибке по управлению.-Передаточная ф-ция в системе по ошибке по возмущению.

8. Статические и астатические системы

Система наз. астатической, если ее сигнал ошибки стремится к нулю при условии, что его управляющие значение стремится к любому ненулевому значению.

,

По теории о конечном значении:

(1)

так,

что , тогда

При

Предел равен нулю тогда и только тогда, когда передаточная функция имеет ноль в начальных координатах.

Передаточная функция имеет ноль порядка, если она представима в виде:

, где .

Для того, чтобы система была статической необходимо и достаточно, чтобы передаточная функция по ошибке имела нуль какого-то порядка в начале координат (представима в выше указанном виде).

Если передаточная функция имеет нуль порядка, то система имеетпорядок статичности.

Следовательно, нуль порядка передаточной функции по ошибке соответствует полюсу того же порядка передаточной функции разомкнутой цепи (в начале координат). Покажем это. Пусть

, тогда .

().

Динамические функции единичной скорости:

(статическая сист.)

9. Типовые воздействия

1. Единичная ступенчатая функция Хевисайда.

- изображение по Лапсасу

В нейронных сетях:

Рассматривается как предел функций.

Дельта-функция

Интервал, в которм произведение больше нуля, он стремиться к началу координат, а площадь остаётся той же (равна 1)

- дельта функция Дирака.

Свойство дельта функции:

Можно заменить x(t) на фактически постоянное значение, т.к.

В частном случае:

Следовательно:

10. Связь между входным и выходным процессами во временной области

Y(S)=X(S)*Ф(S) (1)

По теореме о свертке:

(2)

(3)

Свойства переходной функции:

1. - импульсная переходная функция стремится к нулю с течением времени.

2.

3. Условии физической осуществимости: импульсная функция осуществима, если:

К(t)=0 , при t<0.

Рассмотрим выражение (2)

К(t)=0 , при t<0

К(t-r)=0 , при r>t, следовательно область интегрирования в (2) (по r) может быть продолжена за верхний предел, следовательно

(4)

Рассмотрим выражение (3)

x(t)=0 при t<0 => x(t-r)=0 при r>t =>

=> (5)

(6) – дискретный вариант (5).

:

- импульсная передаточная функция по возмущению.

- импульсная передаточная функция по ошибке.

11. Амплитудно и фазочастотные характеристики (годограф Найквиста)

, A(w)—амплитудная хар-ка, (w)—частотная хар-ка.

На комплексной плоскости можно изобразить частотную характеристику. При любом значении частота W(jw) представляется вектором на комплексной плоскости. Если изм. частоту от 0 до , то этот вектор поворачивается и описывает кривую, наз.годографом.

Для статических систем:

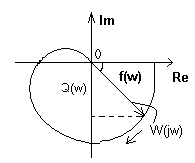
При --действительное число не равно 0, поэтому годограф выходит с т.А Приw→в физич-их системах (n>m) W→0. След-но годограф приходит в т.0

Для астатических систем: . Приw→0 , W→.