21. Спектральные характеристики случайных сигналов и их отличие от спектральных характеристик детерминированных сигналов. Теорема Винера-Хинчина.
Частотные свойства случ. сигналов позволяют эффективно использовать спектральный метод анализа цепей при воздействии на них шумов и помех, успешно решать задачи синтеза систем, обладающих высокой степенью помехозащищенности.
При изучении частотных свойств детерминированных сигналов применялся спектральный анализ , основанный на рядах Фурье для периодических и преобразованиях Фурье для непериодических сигналов. Подобный метод необходим для изучения частотных свойств случ. сигналов.
Непосредственное применение классического метода спектрального анализа для множества реализаций случ. сигнала не представляется возможным , объясняется это тем ,что реализация случ. процесса имеет случайные амплитуды и фазы и их изменения, поэтому усреднение по множеству приводит к нулевому результату.
Выход: применить класс-й метод для энергетических параметров случ. сигнала.
Спектральная плотность мощности
Пусть
– к- я реализация случ. процесса на
интервале [0,Т]. Как известно ,реализация
– неслучайная ф-я.
-
- спектр реализации -
Известно равенство Парсеваля:
-
Рассмотрим это равенство для достаточно длинной реализации: Э=
-
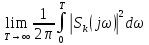
Применим эту формулу для вычисления мощности:
Судя по
полученной формуле можно сказать, что
–
-маленькая
мощность, приходящаяся на –
-маленький
интервал
Тогда
выражение
можно назвать спектральной плотностью
мощности.
В результате
получим
=
– спектральная плотность мощности к-й
реализации.
Учитывая
эргодичность рассматриваемого процесса
=
,
Т – время , а не период.
Полученное выражение позволяет сделать следующие выводы:
-
Спектральная плотность мощности не комплексная , а действительная.
-
-
=[
]=[
]
не содержит информацию о фазах , поэтому
не позволяет восстановить отдельные
реализации случ. процесса.
Иногда
удобно пользоваться нормированной
спектр. Плотностью мощности:
На практике
используют взаимные спектр. Плотности
2-х процессов:
комплексная функция.
Формулы Винера- Хинчина
Определяют связь между частотной и временной хар-ми случ. сигнала. Формулы В-Х относятся к теореме В-Х: «спектральная плотность мощности и ковариационная функция связаны между собой прямым и обратным преобразованиями Фурье».
Доказательство: Пусть x(t) – реализация эргодического СП(она не случайная)
R(
)=
Усредним выражение по времени и учтем , что применительно к СП рассматривается длинная реализация и приведенное выражение соответствует ковариационной функции:
Учитывая,
что
=
,
получаем:
1/2
- это обратное преобразование Фурье
- прямое преобразование Фурье
Если
=0,
то можно записать
, тогда:
1/2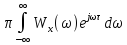
Учитывая
четность
и
можно записать:
1/
Соотношения Винера – Хинчира можно применить для определения спектральной плотности мощности суммы 2-х СП:
Z(t)=x(t)+y(t)
Подставим
братное
преобразование Фурье:
