23. Узкополосные случайные сигналы. Необходимость определения статистических характеристик огибающей и фазы этих сигналов. Законы распределения узкополосного случайного сигнала, его фазы и огибающей.
Узкополосный сигнал (У.с.с.)– сигнал, у которого эффективная ширина полосы частот в любом месте намного меньше центральной частоты.
У.с.с. формируется как результат воздействия случайных явлений различного рода: внешних, искусственных и естественных помех внутр. Шумов.
Вследствие справедливости центральной предельной теоремы: случ. процесс, который является суммой других случ. процессов подчиняется нормальному закону распределения:
Законы распределения огибающей и фазы:
X(t)=U(t)cos(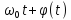
)
– реализация случ. Сигнала
Для
определения закона распределения
огибающей и фазы воспользуемся формулой
реализации с.с.,т.е необходимо найти
P(u),P(
)
Определение
з-на распред-ия p(
)
X(t)=U(t)cos
U(t)sin
=
(t)
-
(t)
,
Где
(t)=
U(t)cos
-косинусная
составляющая
(t)=
U(t)sin
- синусная составляющая
Очевидно,что
U(t)=
=
-arctg
Для
определения p(
)-двумерная
плотность вероятности, найдем P(
)
, P
),
а также особенности случ. процессов
(t)
и
(t).
Анализ
формул для X(t),
(t),
(t)
показывает, что спектры процессов
(t)
и
(t)
отличаются от спектра х(t)
сдвигом частоты
,
при сохранении структуры спектра.
Это
значит, что
(t)
и
(t)
бдут иметь такой же закон распределения,
как и x(t).
Как следует из теоремы Винера-Хинчира:
d
Т.е.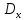
-
площадь под кривой спектральной плотности
мощности
Вывод: т.к.
спектр составляющих сдвинут на
без изменения структуры, то
=
,следовательно:
P(
)=
P
)=
Для
определения p(
)
докажем, что процессы
(t)
и
(t)
независимы:
=
(у зависимых было
бы
+2
)
Корреляц. Ф-я =0.
Значит:
p(
)
=
p(
)
=
Определим
з-н распределения P(U,
)
-
Возьмем бесконечномаленькие фигуры с равной площадью
dUc*dUs=UdUd
-
Как известно вероятность попадания в бесконечномаленький dx равна p(x)dx,следовательно вероятность попадания в прямоугольник dUcdUs равна:
P(Uc,Us)dUcUs =
dUcUs
-
Из другого графика можно записать:
P(U,
)dU
d
- вероятность попадания в dU
d
-
P(Uc,Us)dUcUs =P(U,
)
dUd
-
P(U,
)
=
=
Определение з.р. огибающей
P(U)=
- закон Релея.