3.3.3.2. Сравнение математических ожиданий двух совокупностей

Пусть для двух нормально распределенных генеральных совокупностей с неизвестными параметрами ₁, ₁², и ₂, ₂² испытали выборки объемом N₁ и N₂. По результатам испытаний подсчитали оценки параметров распределения , и , . Требуется установить равенство или неравенство математических ожиданий этих совокупностей ₁ и ₂.

Примем нулевую гипотезу о равенстве математических ожиданий при альтернативной гипотезе об их отличии.

1. Н₀: ₁=₂= ;

2. Н_А: ₁¹₂;

3. Для проверки гипотезы используют t-критерий Стьюдента.

Возможно два случая: А) дисперсии генеральных совокупностей равны, т.е. ₁²=₂²=²; Б) дисперсии генеральных совокупностей не равны, т.е. ₁²¹₂².

А) Дисперсии генеральных совокупностей равны.

4) В этом случае вычисляют оценку общей дисперсии ²:

(3.13)

и статистику . (3.14)

5. Границы критической области можно установить по таблицам квантилей t-распределения (распределения Стьюдента) для выбранного уровня значимости a и числа степеней свободы =N₁+N₂-2 (табл. П6).

6. Нулевую гипотезу принимают при выполнении неравенства .

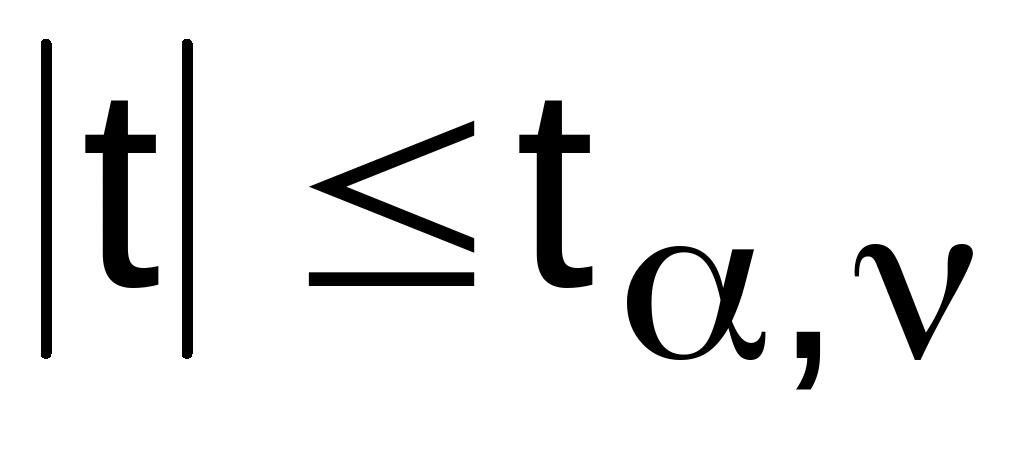Б) Дисперсии генеральных совокупностей не равны (₁²¹₂²).

4) В этом случае оценку общей дисперсии ² вычислять не имеет смысла и t-статистику вычисляют по выражению:

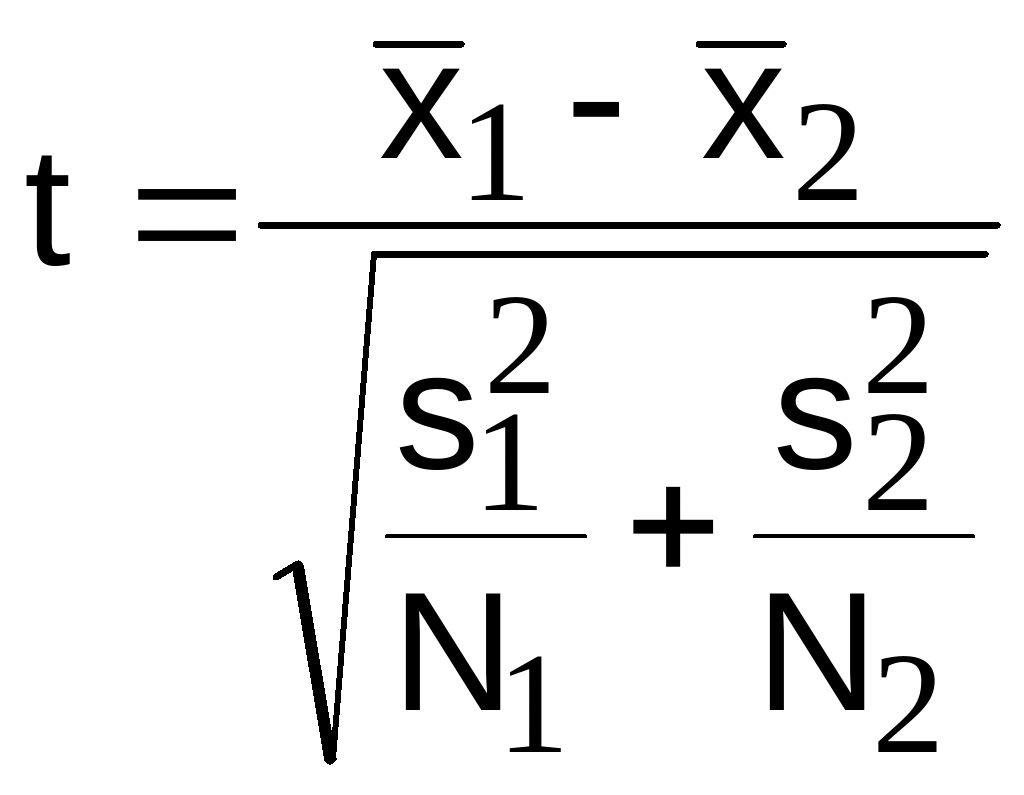. (3.15)

5) Границы критической области можно установить по таблицам квантилей t-распределения (распределения Стьюдента) (табл. П6) для выбранного уровня значимости a и числа степеней свободы  которое определяют из выражения

, (3.16)

где 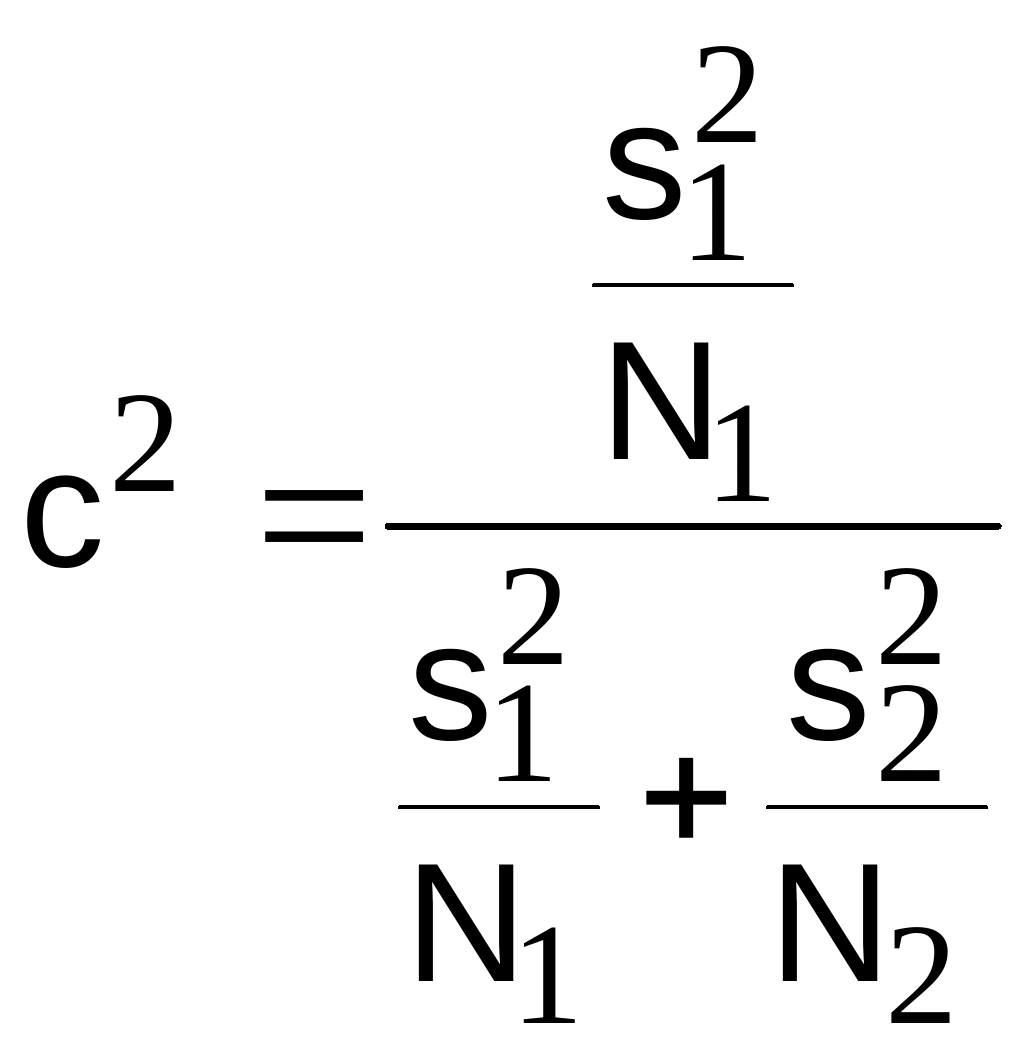. (3.17)

6) Нулевую гипотезу принимают при выполнении неравенства .

В случае принятия нулевой гипотезы Н₀: ₁=₂= по двум выборочным средним производят оценку общего математического ожидания

, (3.18)

которую можно использовать, при дальнейшем анализе опытных данных, например, для построения доверительных интервалов.

3.4. Критерий согласия. Проверка гипотез о виде функции

распределения

Рассмотренные ранее методы оценки случайной величины и проверки гипотез предполагали что известна функция ее распределения – распределения Гаусса. Однако, в большинстве случаев сам вид закона распределения является гипотетическим и нуждается в статистической проверке.

Наиболее простым, но весьма приближенным методом оценки согласия результатов эксперимента с тем или иным законом распределения является графический метод, заключающийся в построении эмпирического закона распределения и сопоставлении его с теоретическим [5]. Если экспериментальные точки лежат вблизи теоретического графика, то опытные данные соответствуют теоретическому закону распределения. Графический метод является в значительной мере субъективным и используется на практике в качестве первого приближения при решении этой задачи.

Более объективным методом установления вида распределения случайной величины является применение критериев согласия. Критерии согласия служат для проверки статистической гипотезы о соответствии генеральной совокупности предполагаемому теоретическому закону распределения на основании анализа выборки опытных данных из этой совокупности. Существует достаточно большое количество критериев согласия [6], отличающихся своей мощностью и объемом опытных данных, необходимых для их использования. Рассмотрим некоторые из них.