3.2.2. Критерий н.В.Смирнова

Этот критерий применяется для наиболее часто встречающихся случаев, когда генеральные характеристики неизвестны, а известны лишь их оценки s² и , произведенные на основании анализируемой выборки. Следует проверить принадлежность результата испытаний x_i генеральной совокупности опытных данных. Используем общий алгоритм из п. 3.1.

1) Нулевая и альтернативная гипотезы принимаются прежними.

Н₀: х_iÎХ .

2) Н₁: х_iÏХ .

3. В качестве статистического критерия используется u -критерий [6].

4. Статистика этого критерия имеет вид 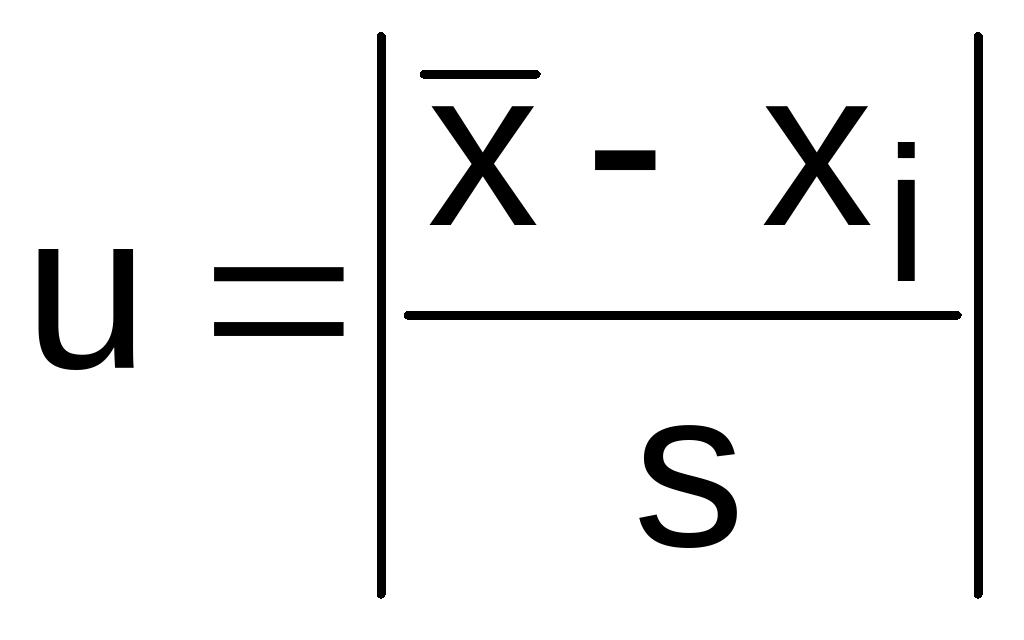, (3.3)

   где s- выборочное стандартное отклонение (2.35).

5. Границы критической области можно установить при помощи критического значения критерия u_{ N}, взятого из табл. П7 приложения для уровня значимости  и объема выборки N.

6. Если выполняется неравенство 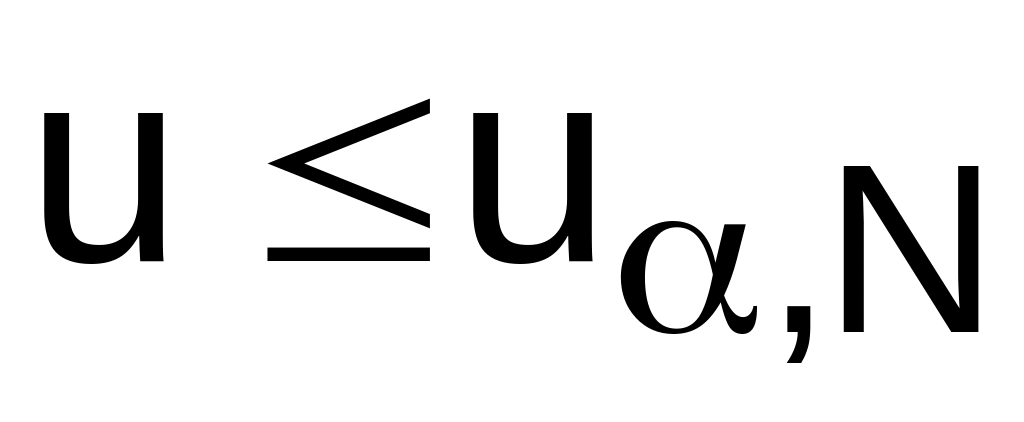, то статистика u попадает в область принятия нулевой гипотезы, результат испытаний x_i не следует считать выбросом и он должен учитываться как и остальные N-1 результатов. При статистика u попадает в критическую область, результат испытаний x_i является ошибочными и должны быть исключены их рассмотрения, а найденная ранее оценка математического ожидания и дисперсии должны быть рассчитаны вновь.

3.3. Проверка гипотез о числовых значениях параметров

нормального распределения

Значения выборочных числовых характеристик случайных величин зависят от размера и состава выборки и так же являются случайными величинами. Следовательно, они сами обладают определенным рассеиванием и собственными вероятностными характеристиками. Поэтому если при расчете оценок числовых характеристик по различным выборкам получено расхождение в числовых значениях, то это еще не означает, что оцениваемые генеральные характеристики этих величин не равны. Просто может оказаться, например, что выборки взяты из различных мест одной и той же генеральной совокупности. Но, так как генеральная совокупность одна, то и ее числовые характеристики едины.

Однако, расхождение может быть и не случайным, а носить вполне закономерный характер.

Часто при решении практических задач возникает необходимость определения значимости или случайности в расхождении выборочных характеристик между собой, а также выборочных и известных генеральных характеристик. Наибольшее практическое значение имеет сравнение средних значений и выборочных дисперсий экспериментально полученных выборок результатов наблюдений и выводы о свойствах соответствующих генеральных характеристик, полученные на основании этих сравнений.

3.3.1. Сравнение двух дисперсий

Гипотезы о равенстве (или неравенстве) дисперсий имеют особо большое значение прежде всего в технике и технологии, так как измеряемая дисперсией величина рассеяния характеризует такие исключительно важные показатели, как точность машин, приборов, стабильность технологических процессов, показатели качества готовой продукции и т.д. Поэтому часто о качестве выпускаемой продукции, преимуществах той или иной технологии можно судить по результатам сравнения дисперсий. При этом возможно несколько вариантов сравнения.