3. Проверка СтатистическИх гипотез

3.1. Статистические гипотезы и критерии согласия

При использовании экспериментальных методов для решении конкретных практических задач часто приходится делать некоторые предположения относительно свойств одной или нескольких генеральных совокупностей основываясь на имеющихся выборках ограниченного объема. Такие предположения являются статистическими гипотезами.

По ГОСТ 15895-77. Статистической гипотезой называют любое предположение, касающееся неизвестного распределения случайной величины в совокупности.

Роль статистических гипотез при обработке экспериментальных данных весьма высока. Без них невозможно обойтись даже при попытке численно охарактеризовать случайную величину на основе выборки, при построении точечных и интервальных оценок.

При построении точечных и интервальных оценок высказывалось предположение, что случайная величина подчиняется нормальному закону распределения. Кроме того, всегда подразумевалось что все выборочные значения принадлежат одной и той же генеральной совокупности (нет резко выделяющихся значений).

Тем более невозможно обойтись без статистических гипотез если возникает задача сравнения двух или более случайных величин.

Идея формирования и проверки статистических гипотез состоит в следующем. Пусть для некоторого числового параметра случайной величины Q по выборке объема N вычислена некоторая оценка . Пусть имеется причина предположить, что истинное значение параметра Q, т.е. его значение в генеральной совокупности, равно Q₀ . Это предположение следует проверить на практике, то есть по имеющимся опытным данным выборки. Такое проверяемое предположение называют нулевой гипотезой Н₀ и записывают в виде соотношения Н₀: Q=Q₀. Даже если нулевая гипотеза справедлива, то выборочное значение обычно не совпадает точно с Q₀ , поскольку оно является лишь одним из конкретных значений случайной величины , порожденной случайными выборками объема N. Если известна функция распределения оценки , построенная теоретически в предположении справедливости нулевой гипотезы, то с ее помощью можно найти такую зону, вероятность попадания в которую мала (равна малому значению ). Эта зона может использоваться в качестве некоторой критической области, то есть области, попадание в которую оценки дает основания отвергнуть выдвинутую нулевую гипотезу.

Нулевой гипотезой обычно называют гипотезу, имеющую наиболее важное значение в проводимом исследовании. Ее обозначают Н₀.

По ГОСТ 15895-77. Нулевая гипотеза это гипотеза, подлежащая проверке.

Нулевую гипотезу выдвигают и затем проверяют с помощью статистических критериев с целью выявления оснований для ее отклонения и принятия альтернативной гипотезы.

По ГОСТ 15895-77. Альтернативная гипотеза - каждая допустимая гипотеза, отличная от нулевой. Ее обозначают Н_А или Н₁.

Обычно при проверке статистических гипотез в качестве конкретной альтернативной гипотезы, из всех возможных, выбирают гипотезу, имеющую в проводимом исследовании второе по важности значение после нулевой.

Если имеющийся статистический материал не позволяет отвергнуть нулевую гипотезу, то ее принимают и используют в качестве рабочей до тех пор, пока новые результаты испытаний не позволяют ее отклонить.

По ГОСТ 15895-77. Статистический критерий - однозначно определенный способ проверки статистических гипотез.

В основе критерия лежит некоторое известное теоретическое распределение случайной величины. По опытным данным рассчитывают некоторую случайную величину, называемую статистикой, относящуюся к данному критерию и имеющую то же распределение .

Статистикой для проверки гипотез называют функцию g(x₁,x₂,...,x_N) результатов наблюдений составляющих выборку x₁,x₂,...,x_N, однозначно связанную с принятым статистическим критерием и определяемую им.

Все возможные значения статистики для проверки гипотезы делят на две части: область принятия нулевой гипотезы и критическую область.

По ГОСТ 15895-77. Критической областью называют область со следующими свойствами: если значения применяемой статистики принадлежит данной области, то отвергают нулевую гипотезу; в противном случае ее принимают.

Проверка гипотезы сводится к выяснению того, в какую область попало рассчитанное значение статистики: если оно попало в критическую область, то нулевая гипотеза отвергается, а если в область принятия нулевой гипотезы, то принимается.

Так как эти решения базируются на статистиках, найденных по выборкам ограниченного объема (то есть на случайных величинах), то при принятии решения всегда возможны ошибки. При статистической проверке гипотез возможны четыре исхода, из них два ошибочные - ошибки первого и второго рода:

Нулевая гипотеза	Объективно верна	Объективно не верна
Принимается	Правильное решение	Ошибка 2-го рода
Отвергается	Ошибка 1-го рода	Правильное решение

По ГОСТ 15895-77. Уровень значимости это вероятность ошибки первого рода. Обозначим уровень значимости через . Обычно выбирают =0.01, =0.1, и наиболее часто =0.05.

Вероятность совершить ошибку второго рода, т.е. принять объективно неверную гипотезу, обозначим . Величину =1- называют мощностью критерия. Обычно величиной  задаются и стараются использовать такой критерий, чтобы значение мощности  было наибольшим.

По ГОСТ 15895-77. Мощность критерия это вероятность того, что нулевая гипотеза будет отвергнута, если альтернативная гипотеза верна.

Критические области бывают односторонние и двухсторонние. Смысл этих областей показан на рис. 3.1.

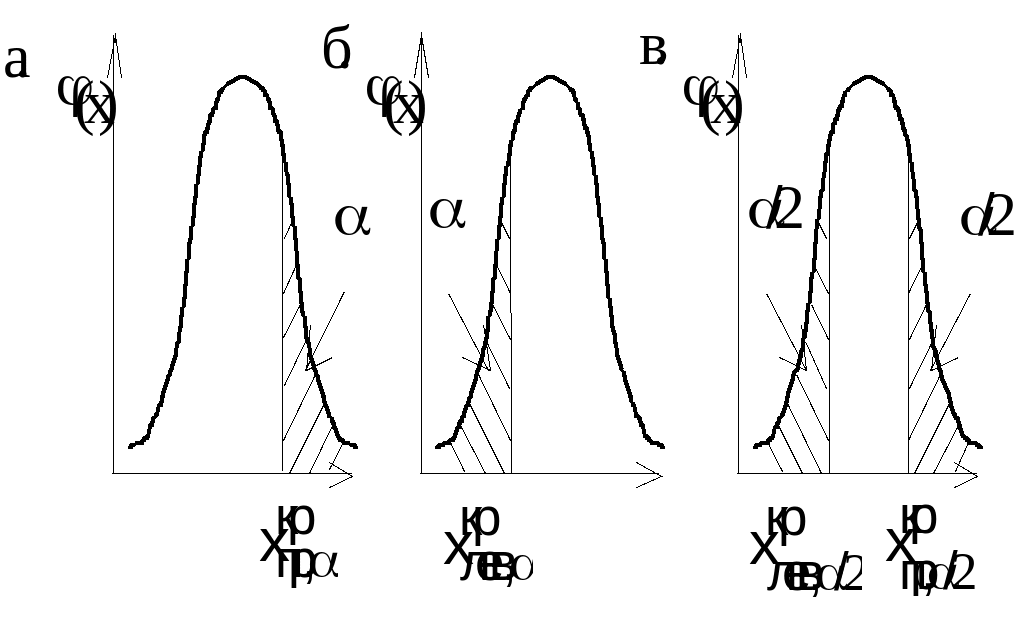Рис. 3.1. Критические области плотности распределения:

а. - правосторонняя; б. - левосторонняя; в. – двусторонняя

Точки, отделяющие области принятия нулевой гипотезы от критических областей называют границами критической области. Обычно их определяют как квантили используемого теоретического распределения, которому подчиняется статистика для проверки гипотез.

Если хотят убедиться в том, что одна случайная величина строго больше другой (или строго меньше другой), то используют одностороннюю критическую область.

В этом случае Н₀: Q=Q₀,

Н₁: Q>Q₀ или Н₁: Q<Q₀.

Если проверяют как положительные, так и отрицательные расхождения между изучаемыми величинами, то используют двусторонние критические области .

В этом случае Н₀: Q=Q₀,

Н₁: Q¹Q₀.

Алгоритм проверки статистических гипотез сводится к последовательному выполнению следующих операций:

1. Формулируют нулевую гипотезу Н₀;

2. Формулируют альтернативную гипотезу Н₁;

3. Выбирают критерий для проверки Н₀;

4. Рассчитывают статистику относящуюся к выбранному критерию;

5. Находят границы критической области при выбранной альтернативной гипотезе Н₁;

6. Проверяют попадание рассчитанной статистики в критическую область и делают вывод о справедливости выдвинутой нулевой гипотезы.

Все последующее рассмотрение будем проводить в соответствии с этим алгоритмом.

При использовании механизма проверки статистических гипотез следует помнить, что даже в случае принятия нулевой гипотезы, в 100×a% случаев вывод будет ошибочным в связи со всегда имеющейся вероятностью совершить ошибку первого рода.