Билет 1

Вопрос 1) Электрическая энергия – это энергия электрического тока во всех его формах, которая распределена в электромагнитном поле.

Поскольку общее определение энергии – это мощность в единицу времени, то единицей измерения электрической энергии является киловатт в час (кВт час). Для характеристики больших объемов производства (электростанции, энергосистемы) используются единицы измерения мегаватт в час (МВт час) и гиговатт в час (ГВт час).

Электрический заряд - физическая величина, определяющая особый тип сил - электромагнитные силы и характеризующая свойство электрически заряженных частиц и тел вступать в электромагнитные взаимодействия.

По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле, которое оказывает силовое действие на другие заряженные тела.

Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Для количественного определения электрического поля водится силовая характеристика - напряженность электрического поля.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:

[Н/Кл]

Напряженность электрического поля – векторная физическая величина. Направление вектора Е  в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.

закона Кулона

сила взаимодействия F в вакууме между двумя неподвижными точечными электрическими зарядами q1 и q2 прямо пропорциональна произведению величин этих зарядов и обратно пропорциональна квадрату расстояния r между ними: где k – коэффициент пропорциональности, зависящий от выбора системы единиц и численно равный силе, с которой два единичных заряда взаимодействуют на единичном расстоянии

Закон Кулона: F=k·q1q2/r2 [Н]

Вопрос 2) Диэлектрическая проницаемость — величина, характеризующая диэлектрические свойства среды — её реакцию на электрическое поле. Она показывает, во сколько раз уменьшится кулоновское взаимодействие зарядов, не испытывающих обратного влияния среды, при переносе их из вакуума в данную среду. Одновременно Д. п.   связывает материальным уравнением   электрич. индукцию D с напряжённостью E электрич. поля в среде.

  В большинстве диэлектриков при не очень сильных полях диэлектрическая проницаемость не зависит от поля Е. В сильных же электрических полях (сравнимых с внутриатомными полями), а в некоторых диэлектриках в обычных полях зависимость D от Е — нелинейная

Так же диэлектрическая проницаемость показывает, во сколько раз сила взаимодействия F между электрическими зарядами в данной среде меньше их силы взаимодействия Fo в вакууме

  

Относительная диэлектрическая проницаемость вещества   может быть определена путем сравнения ёмкости тестового конденсатора с данным диэлектриком (Cx) и ёмкости того же конденсатора в вакууме (Co)

  

Билет 2

Вопрос 1) Ток и напряжение. При включении в цепь переменного тока активного сопротивления R (рис. 175, а) напряжение и источника создает в цепи ток i. Если напряжение и изменяется по синусоидальному закону u = Uт sin ωt, то ток i также изменяется синусоидально:

i = Iт sin ωt

При этом

Iт = Uт / R

Таким образом, ток и напряжение изменяются по одному и тому же закону; они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 175,б). Следовательно, при включении в цепь переменного тока активного сопротивления ток и напряжение совпадают по фазе (рис. 175, в).

Если обе части равенства Iт = Uт / R разделить на , то получим выражение закона Ома для рассматриваемой цепи для действующих значений напряжения и тока:

I = U / R

Следовательно, для цепи переменного тока, содержащей только активное сопротивление, этот закон имеет такую же математическую форму, как и для цепи постоянного тока.

Электрическая мощность. Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см. рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ωt. Изменение мощности происходит с двойной частотой ωt по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ωt = 90° и ωt = 270°

Pmax = UтIт = 2UI

Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)

Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Рср = Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:

W = Pt.

Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому

P = Pmax / 2 = UI

Используя формулу закона Ома, активную мощность можно выразить также в виде P = I2R или P=U2/R.

В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.

Вопрос 2) Рассмотрим электрическую цепь, в которой переменное напряжение u(t) = Um∙sinωt приложено к ёмкости.

Рис.1. Цепь с ёмкостью.

Мгновенное значение тока в цепи с ёмкостью равно скорости изменения заряда на обкладках

конденсатора    i =  , но q = C∙u, то

I = C∙ = ω∙C∙Um∙cosωt = Im∙sin(ωt + π/2), где

ω∙C∙Um = Im.

Мы видим, что в этой цепи ток опережает напряжение на угол π/2. Перейдя к действующим значениям переменного тока I = Im / √2, U = Um / √2, получим:        

 I = U / Xc.

Это закон Ома для цепи переменного тока с ёмкостью, а величина Xc = 1 / ω∙C называется емкостным сопротивлением. Векторная диаграмма для этой цепи:

 

Рис.2. Векторная диаграмма цепи с ёмкостью.

Здесь ток опережает напряжение на π/2.

Посмотрим, что будет представлять собой мгновенная мощность в цепи, содержащей ёмкость.

p(t) = Im∙Um∙sinωt∙sin(ωt + π/2) =  Im∙Um∙sin2ωt.

Временная диаграмма показана ниже.

 

Рис.3.Временная  диаграмма изменения мгновенной мощности в цепи с индуктивностью.

Мы видим, что мгновенная мощность изменяется с удвоенной частотой. При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные - возврату запасённой энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергии между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность является реактивным сопротивлением.

Билет 3

Вопрос 1)  Источник ЭДС это активный элемент цепи, который имеет два вывода. Напряжение на этих выводах не зависит от сопротивления цепи, в которую он включен. То есть независимо от того какой ток будет создавать источник ЭДС в цепи напряжение на его выводах не изменится.  Считается, что внутри источника ЭДС отсутствуют пассивные элементы, такие как активное сопротивление, индуктивность и емкость. То есть можно сказать, что внутренне сопротивление источника ЭДС равно нулю.   В реальных же источниках ЭДС всегда присутствует внутренне сопротивление. Таким образом, при замыкании выводов между собой падение напряжения на внутреннем сопротивлении уравновешивает ЭДС источника. Следовательно, ток короткого замыкания будет иметь какую-то конечную величину.

Рис. 1 - Источник ЭДС реальный

 На схеме реальный источник обозначается как источник ЭДС с включенным последовательно сопротивлением. Его значение подбирается так чтобы отобразить поведение реального источника. Как правило, величина этого внутреннего сопротивления ничтожна, мала и может не браться в рассмотрение. Хотя все зависит от поставленной задачи и конкретной цепи.

 Вольтамперная характеристика реального источника :

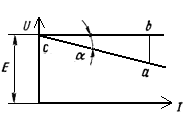
Рисунок 2 —  Вольтамперная характеристика реального источника ЭДС

   При увеличении тока в цепи происходит снижение ЭДС участок ac. Участок ab равен падению напряжения на внутреннем сопротивлении. ab=IR. Участок bc равен току в цепи. Следовательно, тангенс угла альфа будет равен внутреннему сопротивлению tga=R.