Основні теоретичні відомості
Диференціальне рівняння ланки в операторній формі
.
Йому
відповідає характеристичне рівняння
,
яке
має два кореня:
.
Якщо
,
то обидва кореня речові негативні,
перехідна
функція ланки має монотонний, аперіодичний
характер і ланку
називають апериодичним
другого порядку.
Якщо
,
то корені характеристичного рівняння
комплексні:
,
де
;
.
Рішення диференціального рівняння в
цьому випадку містить гармонійні
складові та ланка називають коливальним.
Диференціальне рівняння коливальної
ланки записують зазвичай в наступному
вигляді:
,
де
-
постійна часу, що характеризує інерційність
ланки;
-
відносний коефіцієнт демпфірування
(загасання), що характеризує коливальність
ланки
.
Методичні вказівки
1. Перехідну характеристику аперіодичної ланки другого зарядка (рис. 2.1, а) розраховують за рівнянням
,
де
.
3. Перехідна функція коливального ланки (рис. 1.1, б)
де - коефіцієнт загасання; - власна частота коливань ланки.
Рис.2.1
Цей вираз можна представити в іншому виде:
,
де
.
4. Частотні характеристики ланки (рис. 2.2) розраховують по частотної передавальної функції
.
Виділяючи речову та уявну частини, одержуємо
,
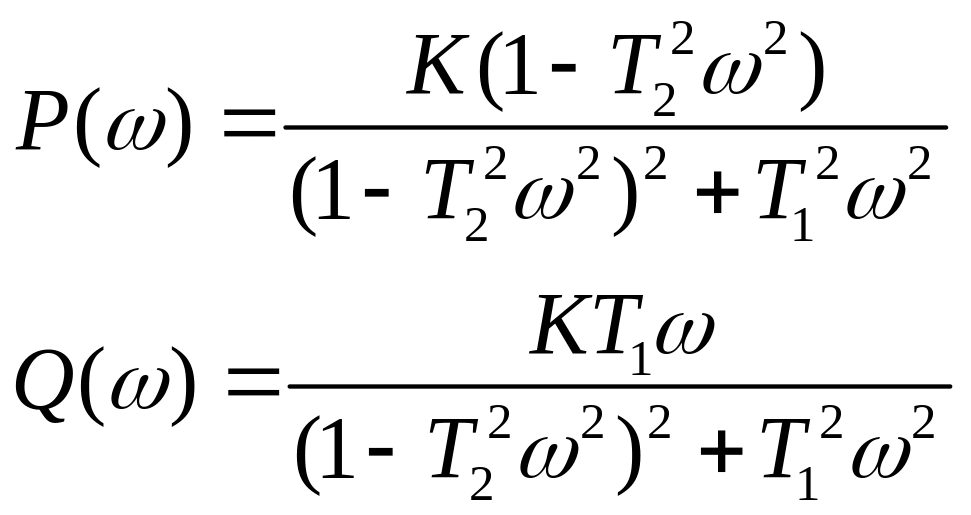Амплітудно-частотну характеристику (рис. 2.2, б)
Рис.2.2
Фазово-частотна
характеристика (рис. 2.2,
в) змінюється монотонно від 0 до
і має вигляд
,
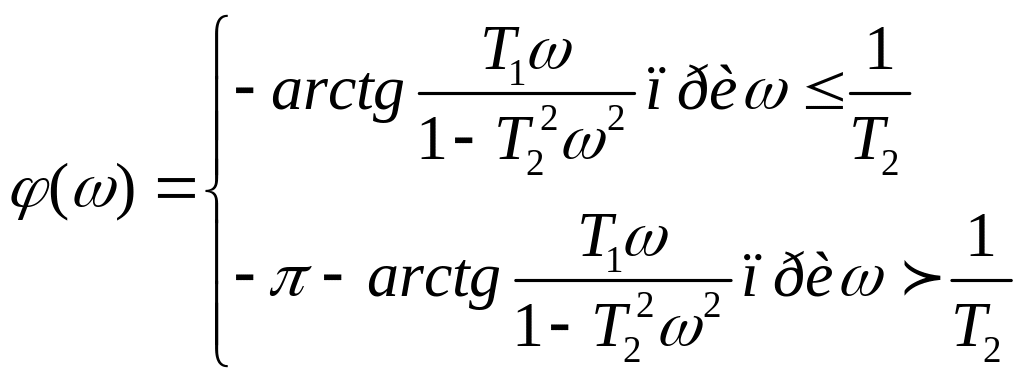Зміст звіту
1. Схема набору і розрахунок параметрів моделі.
2. Початкове диференціальні рівняння, що описують ланку і її модель.
3.
Графік
зміни в часі змінної
.
4. Графік зміни реальної змінної .
5. Графік теоретично розрахованого перехідного процесу ланки
при .
6. Частотні характеристики ланки.
Приклад створення програмного додатку.
Структурна схема моделі
Графік перехідного процесу
Для моделі 1
Для моделі 2
Розрахунок і побудова графіків частотних характеристик
АФЧХ
Передавальна
функція
ланки
Дійсна частина Уявна частина
|
|
|
|
АЧХ
|
|
ФЧХ
|
|
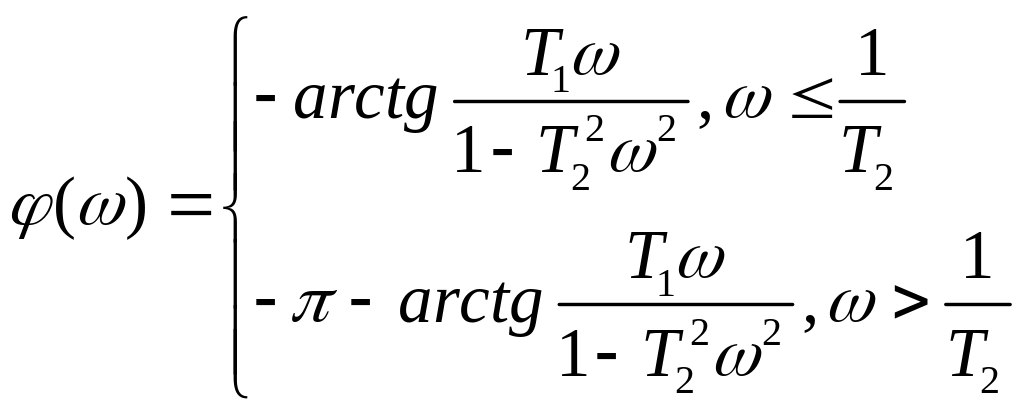
Лабораторна робота № 3
ДОСЛІДЖЕННЯ ДИНАМІЧНИХ ХАРАКТЕРИСТИК
ІНЕРЦІЙНОГО ДИФЕРЕНЦІЮЮЧОЇ ЛАНКИ
Мета роботи - скласти схему набору й експериментально дослідити перехідну функцію інерційного диференціюючого ланки; побудувати теоретично розраховані частотні характеристики.