Математика Контрольная работа № 1 вариант № 1

1. Решить систему линейных уравнений по правилу Крамера:

.

2. Решить систему линейных уравнений методом Гаусса:

.

3. Даны векторы , , ,

из данных векторов выбрать пару ортогональных, тройку компланарных,

найти проекцию вектора 2 - на вектор

4. В треугольнике АВС, где А(4,5), В , С , найти

угол А,

длину медианы АМ и уравнение высоты ВН,

площадь треугольника АВМ.

5. Доказать, что прямые и = = параллельны и найти расстояние между ними.

6. Найти точку М', симметричную точке М(8,9,-1) относительно плоскости .

7. Определить тип кривой . Найти координаты фокусов (фокуса), уравнения директрис (директрисы) и асимптот (если есть). Построить эскиз кривой.

8. Определить угол между плоскостью, касающейся сферы 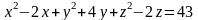в точке А , и прямой, проходящей через начало координат и центр сферы.

Математика Контрольная работа № 1 вариант № 2

1.Решить систему линейных уравнений по правилу Крамера:

2. Решить систему линейных уравнений методом Гаусса:

.

3. Даны векторы , , ,

1) из данных векторов выбрать а) пару коллинеарных, б) тройку компланарных,

2)найти направляющие косинусы вектора

4.В треугольнике АВС, где , , , найти

1) угол А,

2) длину высоты ВН и уравнение медианы АМ,

3) площадь треугольника АВН.

5. Определить взаимное расположение прямой и плоскости (если пересекаются – найти точку пересечения).

6. Найти точку М', симметричную точке относительно прямой .

7. Определить тип кривой . Найти координаты фокусов (фокуса), уравнение директрис (директрисы) и асимптот (если есть). Построить эскиз кривой.

8. Определить угол между плоскостью, касающейся сферы в точке , и прямой, проходящей через начало координат и центр сферы.

Математика Контрольная работа № 1 вариант № 3

1. Решить систему линейных уравнений по правилу Крамера:

.

2. Решить систему линейных уравнений методом Гаусса:

.

3. Даны векторы , , ,

1) из данных векторов выбрать а) пару ортогональных, б) тройку компланарных,

2) найти проекцию вектора на вектор .

4. В треугольнике АВС, где , , найти

1) угол А,

2) длину медианы АМ и уравнение высоты ВН,

3) площадь треугольника АВМ.

5. Доказать, что прямые , , и пересекаются и найти точку их пересечения.

6. Найти точку М', симметричную точке относительно плоскости ω: .

7. Определить тип кривой . Найти координаты фокусов (фокуса), уравнение директрис (директрисы) и асимптот (если есть). Построить эскиз кривой.

8. Определить угол между плоскостью, касающейся сферы в точке , и прямой, проходящей через начало координат и центр сферы.

Математика

Контрольная работа № 1

ВАРИАНТ № 4

1. Решить систему линейных уравнений по правилу Крамера:

.

2. Решить систему линейных уравнений методом Гаусса:

.

3.Даны векторы , , ,

1) из данных векторов выбрать а) пару коллинеарных, б) тройку компланарных,

2) найти направляющие косинусы вектора

4. В треугольнике АВС, где , , , найти

1) угол А,

2) длину высоты ВН и уравнение медианы АМ,

3) площадь треугольника АВН.

5. Определить взаимное расположение прямой и плоскости (если пересекаются – найти точку пересечения)

6. Найти точку М', симметричную точке относительно прямой

7. Определить тип кривой Найти координаты фокусов (фокуса), уравнение директрис (директрисы) и асимптот (если есть). Построить эскиз кривой.

8. Определить угол между плоскостью, касающейся сферы в точке , и прямой, проходящей через начало координат и центр сферы.

Математика

Контрольная работа № 1

ВАРИАНТ № 5

1. Решить систему линейных уравнений по правилу Крамера:

.

2. Решить систему линейных уравнений методом Гаусса:

.

3.Даны векторы , , ,

1) из данных векторов выбрать а) пару ортогональных, б) тройку компланарных,

2) найти проекцию вектора на вектор .

4. В треугольнике АВС, где А(7,8), В(-1,6), С(6,6), найти

1) угол А,

2) длину медианы АМ и уравнение высоты ВН,

3) площадь треугольника АВМ.

5. Доказать, что прямые , , , и параллельны и найти расстояние между ними.

6. Найти точку М', симметричную точке М(4,-5,4) относительно плоскости ω: .

7. Определить тип кривой . Найти координаты фокусов (фокуса), уравнение директрис (директрисы) и асимптот (если есть). Построить эскиз кривой.

8. Определить угол между плоскостью, касающейся сферы в точке А(-2,4,1), и прямой, проходящей через начало координат и центр сферы.