
Задача 4+
Однофакторный эксперимент. Равномерный симметричный план (РСП)
Теория с примерами (кратко)
1.
Однофакторное
ортогонализированное
уравнение
регрессии второго
порядка, в котором все 3 фактора
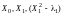 ортогональны,
имеет вид
ортогональны,
имеет вид
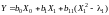 . (1)
. (1)
2.
Ортогонализирующий коэффициент
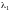 для ортогонализации квадратичного
фактора
для ортогонализации квадратичного
фактора
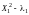 рассчитывается по формуле (
рассчитывается по формуле ( – число
опытов)
– число
опытов)
 .
для
РСП (2)
.
для
РСП (2)
3. Для расчета
ортогонализирующего
коэффициента
,
коэффициентов
уравнения регрессии
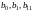 и их доверительных интервалов
и их доверительных интервалов
 для РСП
можно использовать формулы:
для РСП
можно использовать формулы:
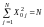 , (3)
, (3)
 . (4)
. (4)
 . (5)
. (5)
4.
Натуральные значения фактора
 заданы на отрезке
заданы на отрезке
 .
Взаимосвязь нормированных значений
фактора Х1
с натуральными х1
определяется следующими формулами:
.
Взаимосвязь нормированных значений
фактора Х1
с натуральными х1
определяется следующими формулами:
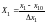 ; (6)
; (6)
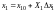 ; (7)
; (7)
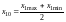 ; (8)
; (8)
 , (9)
, (9)
где
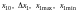 – основной
уровень, интервал варьирования,
максимальное и минимальное натуральные
значения фактора х1,
соответственно. Из уравнений (6) – (9)
следует, что если
– основной
уровень, интервал варьирования,
максимальное и минимальное натуральные
значения фактора х1,
соответственно. Из уравнений (6) – (9)
следует, что если
 ,
то
,
то
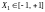 .
.
5.
Матрица планирования (МП) – таблица
для построения однофакторного
ортогонализированного уравнения
регрессии второго порядка, состоящая
из N опытов с числом дублей n в
каждом опыте, включает в себя столбцы:
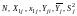 .
Значения
.
Значения
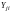 (значение параметра Y
в j-ом опыте и в i-ом
дубле) позволяют провести предварительную
обработку экспериментальных данных:
расчет выборочных средних
(значение параметра Y
в j-ом опыте и в i-ом
дубле) позволяют провести предварительную
обработку экспериментальных данных:
расчет выборочных средних
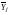 и выборочных дисперсий
и выборочных дисперсий
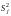 в каждом опыте, проверку выборочных
дисперсий на однородность по критерию
Кохрена, расчёт дисперсии воспроизводимости
в каждом опыте, проверку выборочных
дисперсий на однородность по критерию
Кохрена, расчёт дисперсии воспроизводимости
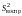 и её числа степеней свободы
и её числа степеней свободы
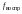 .
Число опытов
должно быть больше числа коэффициентов
уравнения регрессии. Число опытов
.
Число опытов
должно быть больше числа коэффициентов
уравнения регрессии. Число опытов
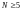 позволяет рассчитать все 3 коэффициента
однофакторного ортогонализированного
уравнения регрессии второго порядка
и обеспечивает надежную проверку
уравнения регрессии на адекватность.
позволяет рассчитать все 3 коэффициента
однофакторного ортогонализированного
уравнения регрессии второго порядка
и обеспечивает надежную проверку
уравнения регрессии на адекватность.
Для построения однофакторного ортогонализированного уравнения регрессии второго порядка будем создавать МП на базе равномерного симметричного плана (РСП), в котором натуральные значения варьируются на равноотстоящих друг от друга уровнях:
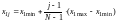 ,
,
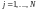 . (10)
. (10)
С учётом уравнений
(6) – (9) нормированные
значения фактора
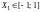 на базе
РСП имеют следующие значения:
на базе
РСП имеют следующие значения:
 ,
. (11)
,
. (11)
NB! Нормированные
значения фактора
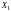 зависят только
от числа опытов N
и не зависят от интервала варьирования
натурального значения фактора
зависят только
от числа опытов N
и не зависят от интервала варьирования
натурального значения фактора
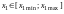
5.1. Предварительная
обработка экспериментальных данных в
МП
на базе РСП для N ‑ опытов
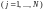 и n – дублей
в каждом опыте
и n – дублей
в каждом опыте
 .
.
5.1.1 Расчёт выборочных параметров:
‑ выборочное
среднее
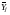 в каждом опыте
в каждом опыте
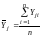 ,
; (12)
,
; (12)
‑ выборочная дисперсия в каждом опыте
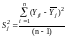 ,
. (13)
,
. (13)
5.1.2. Проверка
выборочных дисперсий на однородность
по критерию Кохрена при условии, что
объём всех выборок одинаковый
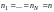 :
:
‑ экспериментальное
значение критерия Кохрена
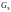 равно
равно
 ; (14)
; (14)
‑ табличное
значение критерия Кохрена
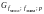 ,
в котором на первом месте стоит число
степеней свободы
,
в котором на первом месте стоит число
степеней свободы
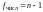 максимальной дисперсии, а на втором ‑ число
степеней свободы
максимальной дисперсии, а на втором ‑ число
степеней свободы
 ,
равное числу всех дисперсий при
доверительной вероятности,
,
равное числу всех дисперсий при
доверительной вероятности,
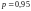 выбирается из таблицы приложения 5;
выбирается из таблицы приложения 5;
‑ выборочные
дисперсии
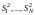 с вероятностью однородны,
если
с вероятностью однородны,
если
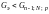 ; (15)
; (15)
‑ выборочные дисперсии неоднородны, если
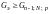 . (16)
. (16)
5.1.3. Если число
дублей
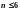 ,
то проверку случайных значений выборки
на промах и на принадлежность их к
нормальному закону распределения можно
не производить.
,
то проверку случайных значений выборки
на промах и на принадлежность их к
нормальному закону распределения можно
не производить.
5.1.4. Если все выборочные дисперсии однородны, то дисперсия воспроизводимости и ее число степеней свободы рассчитывают по формулам:
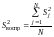 ; (17)
; (17)
 . (18)
. (18)
6. Матрица
моделирования (ММ) – таблица
для построения
однофакторного
ортогонализированного
уравнения регрессии второго
порядка, состоящая из N
опытов (
)
с числом дублей n
(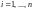 ),
включает в себя столбцы
),
включает в себя столбцы
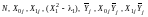 ,
,
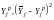 ,
значения которых позволяют провести
окончательную обработку экспериментальных
данных: расчет коэффициентов уравнения
регрессии
,
значения которых позволяют провести
окончательную обработку экспериментальных
данных: расчет коэффициентов уравнения
регрессии
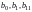 и их доверительных интервалов
и их доверительных интервалов
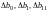 ,
расчёт дисперсии адекватности
,
расчёт дисперсии адекватности
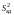 и
её числа степеней свободы
и
её числа степеней свободы
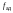 ,
проверку уравнения регрессии на
адекватность, расчет абсолютной ошибки
прогнозирования изучаемого параметра.
Столбец нормированного фактора
,
проверку уравнения регрессии на
адекватность, расчет абсолютной ошибки
прогнозирования изучаемого параметра.
Столбец нормированного фактора
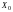 состоит из элементов
состоит из элементов
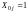 .
Столбец нормированных значений фактора
в ММ
переносятся из МП.
.
Столбец нормированных значений фактора
в ММ
переносятся из МП.
6.1.
Так как уравнение регрессии должно
состоять только
из ортогональных факторов, то прежде
чем рассчитывать коэффициенты
регрессии и их доверительные интервалы,
необходимо
убедиться в том, что факторы
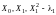 взаимно ортогональны (доказать
самостоятельно при решении задачи
своего варианта).
взаимно ортогональны (доказать
самостоятельно при решении задачи
своего варианта).
Определение: факторы ортогональны, если выполняются равенства:
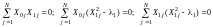 . (19)
. (19)
6.2.
Коэффициенты
однофакторного
ортогонализированного
уравнения
регрессии второго
порядка
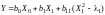 ,
с учётом того,
что факторы
ортогональны, рассчитывают по формулам:
,
с учётом того,
что факторы
ортогональны, рассчитывают по формулам:
 ; (20)
; (20)
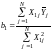 . (21)
. (21)
 . (22)
. (22)
Для расчета
коэффициентов
,
используя вспомогательные столбцы ММ
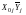 ,
,
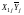 ,
,
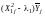 ,
рассчитывают сумма
,
рассчитывают сумма
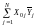 ,
,
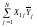 ,
,
 .
Суммы квадратов факторов
.
Суммы квадратов факторов
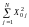 ,
,
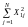 ,
,
 можно
получить прямым подсчетом соответствующих
столбцов ММ
или по формулам (3) – (5).
можно
получить прямым подсчетом соответствующих
столбцов ММ
или по формулам (3) – (5).
6.3. Проверка коэффициентов однофакторного ортогонализированного уравнения регрессии второго порядка на значимость. Дисперсии значимости коэффициентов однофакторного ортогонализированного уравнении регрессии второго порядка при условии, что факторы ортогональны, рассчитывают по формулам:
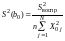 ; (23)
; (23)
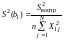 . (24)
. (24)
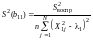 . (25)
. (25)
6.4. Доверительные интервалы коэффициентов однофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по критерию Стьюдента:
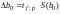 ; (26)
; (26)
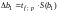 ; (27)
; (27)
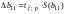 ; (28)
; (28)
где
 – табличное
значение критерия Стьюдента при числе
степеней свободы
– табличное
значение критерия Стьюдента при числе
степеней свободы
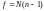 и доверительной вероятности
выбирается из таблицы приложения 2.
и доверительной вероятности
выбирается из таблицы приложения 2.
6.5. Коэффициенты однофакторного ортогонализированного уравнения регрессии второго порядка значимы, если выполняются следующие неравенства:
 ; (29)
; (29)
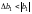 ; (30)
; (30)
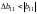 . (31)
. (31)
Регрессионный коэффициент, для которого указанное неравенство не выполняется, следует исключить из полученного уравнения регрессии.
6.6. Проверка однофакторного ортогонализированного уравнения регрессии второго порядка на адекватность.
Дисперсия адекватности и её число степеней свободы для однофакторного ортогонализированного уравнения регрессии второго порядка рассчитывают по формулам:
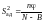 ; (32)
; (32)
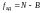 ; (33)
; (33)
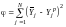 ; (34)
; (34)
где
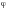 – остаточная
сумма квадратов; N – число
опытов; n – число
дублей в каждом опыте;
– остаточная
сумма квадратов; N – число
опытов; n – число
дублей в каждом опыте;
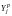 (
) – расчётные
значения параметра Y
по однофакторному
ортогонализированного
уравнению регрессии второго
порядка
(
) – расчётные
значения параметра Y
по однофакторному
ортогонализированного
уравнению регрессии второго
порядка
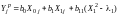 ,
в котором только значимые коэффициенты;
В – число
значимых коэффициентов однофакторного
уравнения регрессии второго
порядка.
,
в котором только значимые коэффициенты;
В – число
значимых коэффициентов однофакторного
уравнения регрессии второго
порядка.
Проверка
однофакторного
ортогонализированного
уравнения
регрессии любого
порядка на
адекватность сводится к проверке
дисперсий
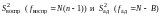 на однородность по
критерию Фишера:
на однородность по
критерию Фишера:
‑ экспериментальное
значение критерия Фишера
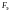 (отношение бльшей
дисперсии к мньшей)
(отношение бльшей
дисперсии к мньшей)
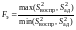 ; (35)
; (35)
‑ табличное
значение критерия Фишера
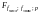 ,
в котором на первом месте стоит число
степени свободы
,
в котором на первом месте стоит число
степени свободы
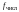 бльшей
дисперсии, а на втором ‑ число
степени свободы
бльшей
дисперсии, а на втором ‑ число
степени свободы
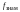 мньшей
дисперсии, при доверительной вероятности
и выбирается из
таблицы приложения 4;
мньшей
дисперсии, при доверительной вероятности
и выбирается из
таблицы приложения 4;
‑ однофакторное ортогонализированное уравнение регрессии любого порядка адекватно, если
 ; (36)
; (36)
‑ однофакторное ортогонализированное уравнение регрессии любого порядка неадекватно, если
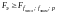 . (37)
. (37)
7.
Если полученное однофакторное
ортогонализированное
уравнение
регрессии второго
порядка адекватно,
то абсолютная погрешность
 для параметра
для параметра
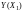 ,
рассчитанного по уравнению регрессии
,
равна:
,
рассчитанного по уравнению регрессии
,
равна:
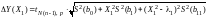 , (38)
, (38)
где – табличное значение критерия Стьюдента при числе степеней свободы и доверительной вероятности выбирается из таблицы приложения 2.
8.
Параметр Y,
описываемый однофакторным
ортогонализированным
уравнением регрессии второго
порядка всегда
имеет экстремум: максимум
при
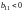 ,
или минимум
при
,
или минимум
при
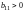 .
Необходимое условие максимума
(минимума) – равенство нулю первой
производной –
.
Необходимое условие максимума
(минимума) – равенство нулю первой
производной –
 ,
Продифференцировав однофакторное
ортогонализированное
уравнение регрессии второго
порядка
по фактору X1
и приравняв к нулю первую производную
,
получим следующее уравнение для расчета
оптимального значения фактора X1
,
Продифференцировав однофакторное
ортогонализированное
уравнение регрессии второго
порядка
по фактору X1
и приравняв к нулю первую производную
,
получим следующее уравнение для расчета
оптимального значения фактора X1
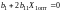 , (39)
, (39)
откуда
 . (40)
. (40)
Соответствующее
натуральное значение фактора
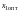 рассчитывается по уравнению (7)
рассчитывается по уравнению (7)
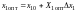 . (41)
. (41)
Максимум (минимум)
параметра
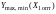 и предельная абсолютная погрешность
и предельная абсолютная погрешность
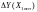 рассчитываются по уравнениям (1) и (40)
рассчитываются по уравнениям (1) и (40)
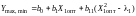 ; (42)
; (42)
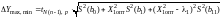 . (43)
. (43)
Типовая задача
Цель: освоить методы моделирования и оптимизации однофакторных технических систем, описываемых стохастическими закономерностями.
Формулировка
задачи.
Зерно, собранное комбайном, имеет
влажность 30 %.
На току оно подсыхает до влажности
20 %.
Для долгосрочного хранения на элеваторе
зерно должно иметь влажность 14 %. Для
сушки зерна до указанной влажности
используют специальные сушила,
теплоносителем в которых является
горячий воздух. Важнейшим параметром,
характеризующим эффективность работы
сушила, является удельный расход энергии
(параметр Y, кВтч/т).
При
прочих равных условиях удельный расход
энергии зависит от температуры
теплоносителя –
горячего
воздуха (фактор х1, С).
Необходимо изучить зависимость удельного
расхода энергии Y
от температуры теплоносителя х1,
варьируемого в интервале
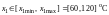 и определить оптимальный режим
функционирования сушила.
и определить оптимальный режим
функционирования сушила.
Математическая формулировка задачи: 1) построить адекватное уравнение регрессии, отражающее зависимость удельного расхода энергии (Y, кВтч/т) от температуры воздуха (х1, С); 2) рассчитать оптимальное значение фактора х1(С), при котором удельный расход энергии Y будет минимальным.
Решение
задачи выполним с помощью однофакторного
уравнения регрессии второго
порядка на базе РСП с числом опытов
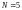 и числом дублей
и числом дублей
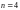 .
Результаты эксперимента приведены в
таблице 1.
.
Результаты эксперимента приведены в
таблице 1.
Таблица 1. – Экспериментальные данные для РСП
N |
х1j, С |
Yj1, кВтч/т |
Yj2, кВтч/т |
Yj3, кВтч/т |
Yj4, кВтч/т |
1 |
60 |
73,5 |
75,3 |
73,5 |
74,1 |
2 |
75 |
60,4 |
60,2 |
63,7 |
61,5 |
3 |
90 |
55,4 |
59,0 |
58,8 |
54,8 |
4 |
105 |
54,8 |
55,5 |
54,3 |
51,9 |
5 |
120 |
59,7 |
62,5 |
57,9 |
57,8 |
План решения задачи с использованием программы Mathcad:
1. Внимательно прочитать условия задачи. Выбрать исходные данные согласно решаемому номеру варианта и ввести их в программу Mathcad.
2. Ввести формулы взаимосвязи натуральных значений фактора х1 с нормированными Х1 для расчета МП.
3. Выполнить предварительную обработку экспериментальных данных:
рассчитать средние значения удельного расхода энергии (Y, кВтч/т) в каждом опыте;
рассчитать дисперсии значения удельного расхода энергии (Y, кВтч/т) в каждом опыте;
проверить однородность дисперсий по критерию Кохрена;
рассчитать дисперсию воспроизводимости эксперимента.
4. Рассчитать и записать в отчет МП для построения однофакторного ортогонализированного уравнения регрессии второго порядка:
рассчитать ортогонализирующий коэффициент ;
ввести фиктивный фактор
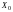 ;
;рассчитать значения фактора
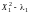 .
.
5. Создать ММ для построения однофакторного ортогонализированного уравнения регрессии второго порядка и выполнить окончательную обработку экспериментальных данных:
рассчитать коэффициенты однофакторного ортогонализированного уравнения регрессии второго порядка;
рассчитать дисперсии коэффициентов однофакторного ортогонализированного уравнения регрессии второго порядка;
проверить статистическую значимость рассчитанных коэффициентов по критерию Стьюдента.
6.
В случае адекватности однофакторного
ортогонализированного
уравнения регрессии второго
порядка провести оптимизацию изучаемого
объекта: рассчитать оптимальные значения
факторов
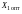 и
,
значение
и
,
значение
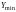 ,
а также абсолютную
ошибку
,
а также абсолютную
ошибку
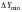 .
.
7. По результатам моделирования и оптимизации изучаемой технической системы сделать вывод.
